Fracture Process Zone
| A service provided by |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Our further education offers: https://www.psm-merseburg.de/weiterbildung |
| PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Fracture process zone
General information
Blumenauer [1] describes that crack propagation is determined by interaction processes between microcracks and morphology, generally referred to as microstructure in metals, in an area close to the crack tip. In most cases, crack propagation in this area is characterised by the formation of microcracks or cavities that merge to form a main crack.
Fracture process zone for plastics
In plastics, crack formation is initiated by local plastic deformations, such as those that occur during the formation of crazes or shear bands. Unlike cracks, crazes contain highly oriented stretched material that forms parallel to the direction of stress. Crazes form when the yield stress is exceeded at points of increased stress concentration (defects in the molecular structure, foreign particles, cavities, etc.).
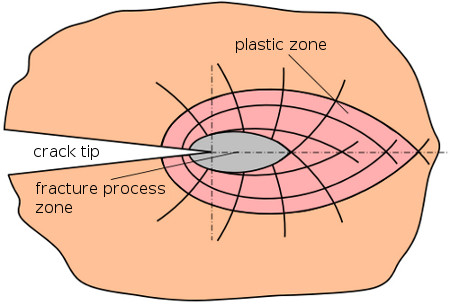
| Fig. 1: | Fracture zone and plastic zone at the crack tip [1] |
This can cause heavily stressed macromolecules to tear open, creating micro-voids. As the crazes continue to grow, the fibrils between the voids are destroyed and a crack spreads along the craze axis. Figure 1 illustrates the geometric relationships between the fracture process zone and the plastic zone.
In contrast to plastics, the fracture zone in brittle crystalline materials is assumed to be very small, often only a few atomic distances in size [1].
Significance for the modelling of particle- and fibre-reinforced plastics
The fracture process zone plays an important role in the development of fracture models for particle composites [2, 3] or fibre-reinforced plastics [4, 5].
To describe the mechanical deformation and crack propagation behaviour, the deformation processes in very extensive process zones with microcracks are the decisive prerequisite for predicting toughness using fracture mechanical material parameters.
In this context, it is particularly noteworthy that the process zone has the same significance as the cohesive zone introduced by Barenblatt [6] in his atomistic crack model (cohesive zone model). This model has proven itself in the modelling of crack propagation in elastic-plastic materials (including plastics), within adhesive and welded joints, and in the delamination of layered materials and components (such as fibre composites and peel films [8]) [7]. The cohesive zone model is also very well suited for the numerical treatment of fracture processes within the framework of the finite element method [7].
See also
- Plastic zone
- Crack tip opening displacement concept
- Fibre-reinforced plastics fracture model
- Energy release rate
- Fracture formation
References
| [1] | Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1993) 3rd Edition, p. 22, (ISBN 3-342-00659-5; see AMK-Library under E 29-3) |
| [2] | Grellmann, W., Bohse, J., Seidler, S.: Bruchmechanische Analyse des Zähigkeitsverhaltens von teilchengefüllten Thermoplasten. Mat.-wiss. und Werkstofftechnik 21 (1990) H. 9, pp. 359−364 |
| [3] | Grellmann, W., Seidler, S., Bohse, J.: Zähigkeit und Morphologie von Thermoplast/Teilchenverbunden. Kunststoffe 81 (1991) H. 2, pp. 157−162 und Toughness and Morphology of Thermoplastic / Particle Composites. Kunststoffe German Plastics 81 (1991) H. 2, pp. 29−32 |
| [4] | Grellmann, W., Lauke, B., Seidler, S.: Application of J-Integral Concept for the Description of Toughness Properties of Fiber Reinforced Polyethylene Thermoplastics. Polymer Composites October Vol. 12, (1991) No. 5, 320−326 |
| [5] | Grellmann, W., Seidler, S., Nezbedova, E.: Analysis of Fracture Behaviour of Fibre Reinforced Polypropylene Using R-Curve Concept. Makromolekulare Chemie, Macromol. Symp. 41 (1991) 195−208 DOI: https://doi.org/10.1002/masy.19910410116 |
| [6] | Barenblatt, G. I.: On Equilibrium Cracks Formed in Brittle Fracture. General Concepts and Hypotheses. Axisymmetric Cracks. Prikladnaya Matematika i Mekhanika 23 (1959) 434‒444 (in Russian); Journal of Applied Mathematics and Mechanics 23 (1959) 622‒636 (english tradition) |
| [7] | Gross, D., Seelig, T.: Bruchmechanik. Mit einer Einführung in die Mikromechanik. 5th Edition, Springer Berlin Heidelberg (2011), (ISBN 978-3-6421-0195-3), Chapter 5.3 Kohäsivzonenmodelle, pp. 156‒160 |
| [8] | Geißler, G., Kaliske, M., Grellmann, W., Nase, M.: Peel Process Simulation of Sealed Polymeric Film – Computational Modelling of Experimental Results. Engineering Computations 24 (2007) 586‒607 |