Fracture Behaviour
| A service provided by |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Our further education offers: https://www.psm-merseburg.de/weiterbildung |
| PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Fracture behaviour, plastics
General information
Depending on the type and stress conditions, polymer materials (see also: plastics) exhibit very different behaviour at break.
Some semi-crystalline polymers such as polyamide (abbreviation: PA), polyethylene (abbreviation: PE) and polypropylene (abbreviation: PP) can be cold-drawn up to an elongation ratio of λ = 20, whereby a stable necking moves along the test specimen.
Many amorphous plastics (e.g. polystyrene (abbreviation: PS)) or polymethyl methacrylate (abbreviation: PMMA) are brittle under tensile stress, but deform plastically under compressive stress or pure shear stress. Epoxy resins (abbreviation: EP) also exhibit a high degree of ductility in compression. Typical examples of ductile and tough fracture behaviour include PP, PE and PA.
Typical mechanisms of plastic deformation
Plastic deformation occurs in two forms in ductile polymers:
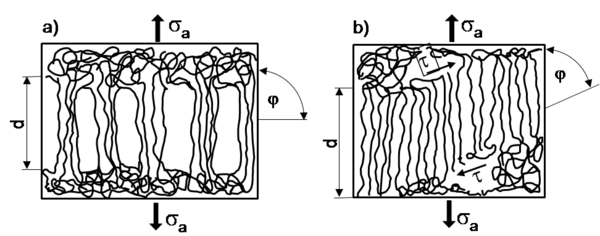
- Shear yielding, i.e. the formation of shear stress flow zones, which causes a strong change in shape without a change in volume. Many semi-crystalline polymers show shear deformation under tensile stress, room temperature (RT) and testing in air (Fig.).
- Crazing (normal stress flow zone formation), i.e. the formation of cavities (see also: micromechanics & nanomechanics) This process causes a strong change in density and occurs in blends and practically all glassy polymers. Individual isolated crazes are often found at low stresses (Fig.).
| Fig.: | Schematic representation of deformation phenomena in amorphous plastics
(a) Craze (see: micromechanics & nanomechanics) |
The occurrence of one or both mechanisms depends on the following conditions:
- Structure of macromolecules
- Degree of crystallisation and spherulite size
- Degree of deformation
- Presence of a second phase and test conditions
- Temperature
- Deformation rate
- Triaxial stress rate
- Ambient conditions
Fracture behaviour, short fibre composites
The use and application limits of short-fibre-reinforced composites are also determined by the need to determine the expected composite properties as precisely as possible in advance. The variety of influencing factors means that a comprehensive theory of the mechanics of polymer composites will not be possible in the future either. It therefore seems most appropriate to describe empirically determined laws using application-orientated, target-oriented models in mathematically simple forms.
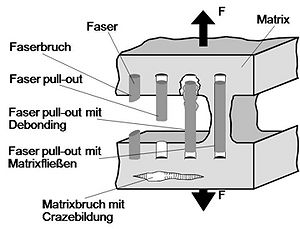
There are numerous attempts in the literature to describe the toughness behaviour of fibre-reinforced composites using models [2, 3]. An essential basic assumption in these models is often a brittle material behaviour (see: fracture types). Based on this, the toughness behaviour was modelled using theoretical concepts, whereby interaction parameters could often not be taken into account. In general, however, the failure process of short fibre-reinforced plastics is characterised by the occurrence of energy-dissipative processes, whereby the mechanisms shown in the figure occur:
- crack runs around fibre
- pull-out
- debonding
- plastic deformation and matrix failure
Fracture behaviour, particle filled thermoplastics
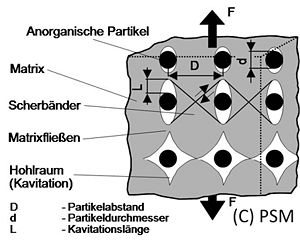
The model by Bohse [4, 5] shows one possibility for modelling the fracture work that is performed in particle-filled thermoplastics with unstable crack propagation and elastic-plastic material behaviour.
In analogy to the model concepts of Friedrich and Lauke [6] for short fibre composites, the following work components occur:
- matrix/particle detachment
- non-linear viscoelastic matrix deformation
- plastic dformation of matrix fibrils
- fibril fracture
See also
- Fracture mechanics
- Fracture behaviour components
- Fracture types
- Micromechanics & Nanomechanics
- Plastics
References
| [1] | Michler, G. H.: Kunststoff-Mikromechanik – Morphologie, Deformation und Bruchmechanismen von polymeren Werkstoffen. Carl Hanser Munich Vienna (1992) ISBN 3-446-170685 (see AMK-Library under F 4) |
| [2] | Friedrich, K. (Ed.): Application of Fracture Mechanics to Composite Materials. Elsevier (Composite Materials Science Volume 6), Amsterdam New York (1989), e-Book ISBN 978-0-4445-9721-2 |
| [3] | Sanadi, A. R., Prasad, S. V. and Rohatgi, P. K.: Sunhemp Fiber-reinforced Polyester. 1. Analysis of Tensile and Impact Properties. J. Material Science 21 (1986)12, 4299–4304; https://doi.org/10.1007/BF01106545 |
| [4] | Grellmann, W., Bohse, J., Seidler, S.: Bruchmechanische Analyse des Zähigkeitsverhaltens von teilchengefüllten Thermoplasten. Materialwissenschaft und Werkstofftechnik 21 (1990) 9, S. 359–364; https://doi.org/10.1002/MAWE.19900210910 |
| [5] | Bohse, J., Grellmann, W., Seidler, S.: Micromechanical Interpretation of Fracture Toughness of Particulate-filled Thermoplastics. J. Material Science 26 (1991) 24, 6715–6721; https://doi.org/10.1007/BF00553697 |
| [6] | Lauke, B., Friedrich, K.: Fracture Toughness Modelling of Fibre Reinforced Composites by Crack Resistance Curves. Adv. Compos. Mater. 26 (1991) 261–275; https://doi.org/10.1016/0266-3538(86)90055-2 |