Ultrasound – Elastic Parameters
| A service provided by |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Our further education offers: https://www.psm-merseburg.de/weiterbildung |
| PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Ultrasound – Elastic parameters
Determination of the elastic parameters with ultrasound
General
The determination of elastic material values by means of ultrasonic measurement technology is a measurement method of non-destructive plastics testing which, under certain conditions, provides more accurate results compared to the tensile test with longitudinal and transverse extensometers than is possible in the material testing machine with mechanical or optical extensometers. In addition, this method is very economical, as it is not only non-destructive, but can also be carried out relatively quickly.
The calculation equations of the modulus of elasticity, the shear modulus, the compression modulus and the Poisson's ratio are derived from the theory of elasticity, which contain the mass density and the longitudinal and transverse sound velocities of the tested material [1].
These equations apply exactly to materials with linear-elastic behaviour such as metals and ceramics and can therefore only be used approximately for heterogeneous materials. For plastics, it should be noted that due to their viscoelasticity – and also the heterogeneity of the semi-crystalline polymers – a high sound attenuation is generally to be expected, and stronger scattering occurs in the measurement series [2, 3]. That's why lower measuring frequencies are to be used for these materials, whereby the inhomogeneities should be several times smaller than the wavelength, so that the calculation equations, as listed below, are still valid.
Specimen
In order to carry out the measurements, a special geometry of test specimens is necessary, which allows an accurate determination of the longitudinal and transverse ultrasonic velocities. The following figure (Fig. 1) shows a possible geometry.
| Fig. 1: | Prismatic test specimen with bevelled edge |
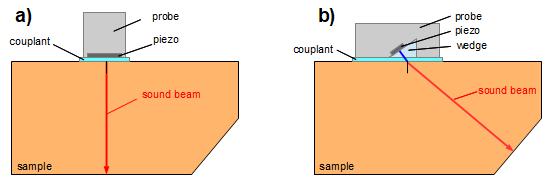
The geometry of a cuboid allows the measurement of both sound velocities, with the bevel adapted to the direction of the sound beam incident from the angle probe (the main axis of the sound field forming) (cf. Fig. 2b). This adjustment is made so that the transverse wave (see also: Refraction of sound waves) hits the bevel perpendicularly.
Measurement of sound velocities
For the measurement of the longitudinal sound velocity cL, a normal probe (also called perpendicular transducer) is used according to the pulse-echo method. It is coupled to the test specimen (according to Fig. 2a) in such a way that the main axis (= acoustic axis) of the developing sound field meets the two opposite plane-parallel surfaces of the test specimen perpendicularly. This means that the acoustic axes of the sound fields of the incoming sound beam and the sound beam returning from the wall are the same, and the speed of sound can be calculated using the formula
| . | (1) |
Within the time tS (sound travel time), the sound wave travels through twice the thickness d.
| Fig. 2: | Prismatic specimen with bevelled edge and coupling of a normal (a) and an angle probe (b) |
To measure the transverse sound velocity cT, the angle probe is aligned so that the sound beam, i.e. the main axis of the sound field, is perpendicular to the bevelled surface (Fig. 2b). The longitudinal sound velocity is determined completely analogously according to formula (1).
Determining the elastic material parameters
The material's moduli (elasticity (E), shear (G), compression (K) modulus) as well as the Poisson's ratio μ result from the relationships between the linear-elastic material parameters and the density ρ as well as the speed of sound. They have the following form:
| (2) |
| (3) |
| (4) |
| (5) |
Strictly speaking, these relations apply to isotropic solids. Thus, these equations are exactly valid for homogeneous (non-porous) ceramics [4]. However, they can also be used as a good approximation to determine the elastic properties of heterogeneous materials. This is always the case when the inhomogeneities (see: damage analysis and component failure) in the materials are small compared to the wavelength at which ultrasonic waves propagate in the material.
Comments on the accuracy of the procedure
The structure of the sound field is different for normal and angle beam probes. The normal probe has an axially symmetrical sound field that tapers off as the nominal frequency of the probe increases. This makes it possible to measure the speed of sound very accurately if both the surface on which the transducer is placed and the sounded boundary surface (see: phase boundary surface) are normal to the axis of the sound field. Here, if the sound attenuation is not too high, the multiple echo method is recommended (see: ultrasonic wall thickness measurement).
The inaccuracies are more likely to occur with the angle probe, whose sound field has a larger divergence angle (see: ultrasonic standard sensors). Thus, according to the distance law , the reflected amplitude of the wave emitted by the angle probe is significantly lower than that of the normal probe. Here I0 represents the intensity of the wave emitted by the probe, I that of the received wave and r the double distance between probe and reflecting surface. This sound attenuation is therefore greater with the angle probe. In addition, the nominal frequency of angle probes is limited to a maximum of 5 MHz [5], which means that the same accuracy cannot be achieved as with a normal probe (≥ 10 MHz). Therefore, the angle probe should first be calibrated to measure the transverse sound velocity.
See also
- Ultrasonic direct coupling
- Pulse-echo ultrasonic technique
- Ultrasonic weld inspection
- Ultrasonic runtime measurement
- Ultrasonic immersion bath technique
References
| [1] | Landau, L. D., Lifschitz, E. M.: Lehrbuch der theoretischen Physik – Elastizitätstheorie Bd. 7, Akademieverlag Berlin (2009) |
| [2] | Krautkrämer, J., Krautkrämer, H.: Die Schwächung von Ultraschallwellen in festen Stoffen. In: Krautkrämer, J., Krautkrämer, H. (Hrsg.): Werkstoffprüfung mit Ultraschall. Springer Verlag Berlin, Heidelberg (1990) (ISBN 978-3-662-1082-2) |
| [3] | Grellmann, W., Bierögel, C., Reincke, K. (Eds.): Wiki „Lexikon Kunststoffprüfung und Diagnostik“ 2025, Version 15, https://wiki.polymerservice-merseburg.de/index.php/Absorption_Schallwellen |
| [4] | DIN EN 843-2 (2007): Hochleistungskeramik – Mechanische Eigenschaften monolithischer Keramik bei Raumtemperatur – Teil 2: Bestimmung des Elastizitätsmoduls, Schubmoduls und der Poissonzahl |
| [5] | Waygate Technologies – Baker Hughes Company.: Ultraschallprüfköpfe für Fehlernachweise und Größenbestimmungen. Baker Hughes Company (2020) https://www.bakerhughesds.com/sites/g/files/cozyhq596/files/2020-07/bhcs34592-de_ultrasonic_transducers_catalog_r9.pdf (Zugriff am 06.02.2023) |