J-Integral Concept

Sprachauswahl/Language selection

Dieser Artikel ist auch auf Deutsch verfügbar J-Integral-Konzept

A service provided by
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Our further education offers: https://www.psm-merseburg.de/weiterbildung
PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

J-integral concept

Energetic consideration of the fracture process

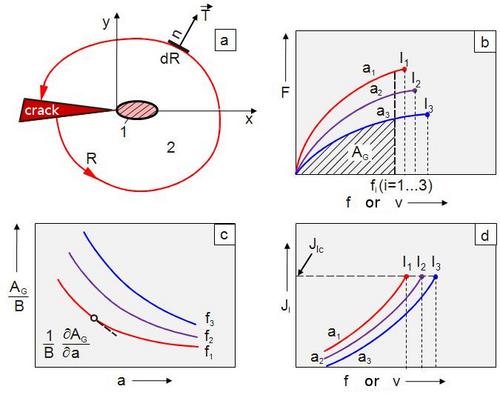
The J-integral introduced by Cherepanov [1] and Rice [2] has gained the greatest importance for plastics due to the energetic consideration of the fracture process (see: Fracture mechanics and types of fracture). The path-independent contour integral encloses the plastically deformed region and runs in the elastic deformed region with a closed integration path around the crack tip (Figure 1).

Fig. 1:

Determination of the J-integral: path-independent contour integral with 1 – plastically deformed area (energy-dissipative zone) and 2 – elastically deformed area (a), experimentally determined load vs. load-line displacement curves of different crack lengths (b), energy determined by planimetrating the dependency F = F(v, f) dependence, related to the specimen thickness as a function of the crack length (c) and J-integral (d) determined by differentiating the curves (c) [3].

The x- und y-components are defined by

$J_{x}\,=\,\int _{R}\left(W\,dy-T_{ij}\cdot n_{j}{\frac {\partial u}{\partial x}}dR\right)$ und

$J_{y}\,=\,\int _{R}\left(-W\,dx-T_{ij}\cdot n_{j}{\frac {\partial u}{\partial x}}dR\right)$.

with

W		elastic energy density
T		stress tensor
n		components oft the unit vector to R around the crack tip
u		displacement vector components

Experimental determination of J-values

The experimental determination is carried out according to Fig. 1 b to d by determining the deformation energy A_G from the registered load vs. load line displacement curves with different notch depths by planimetry and displaying the ratio A_G/B as a function of a. The deformation energy A_G is then determined by the graphical differentiation.

Using graphical differentiation, the following results

$J\,=\,{\frac {1}{B}}{\frac {\partial A_{G}}{\partial a}}$

as function of the load-line displacement resp. deflection.

Since the effort to determine J-values according to this procedure is too high for practical characteristic value determination, approximation formulas have been developed. The best-known procedures are:

• Approximation method according to BEGLEY and LANDES,
• Approximation method according to RICE, PARIS and MERKLE,
• Approximation method according to KANAZAWA ,
• Approximation methods according to SUMPTER and TURNER and
• Approximation methods according to MERKLE and CORTEN.

Correlations of the J-integral to the stress intensity factor and the crack opening displacement

For elastic material behaviour, the J-integral is identical to the energy release rate G:

	$J_{I}\,=\,G_{I}\,=\,{\frac {{K_{I}}^{2}}{E}}$	for ESZ resp.
	$J_{I}\,=\,G_{I}\,=\,{\frac {{K_{I}}^{2}}{E}}\left(1-{\nu }^{2}\right)$	for EDZ.

These equations are to be used for the conversion of J_Ic values into K_Ic^J values.

The relationship between J-integral and Crack tip opening displacement (CTOD) concept provides

$J\,=\,m\cdot \sigma _{y}\cdot \delta _{Ic}$,

where m is called the constraint factor according to [4, 5]. The critical J-values are geometry-independent, i.e. real material values, if the criterion

$B{,}\ a{,}\ \left(W-a\right)\,\geq \,\varepsilon {\frac {J}{\sigma _{y}}}$

with

$\varepsilon \!$

material-dependent constant of the geometry criterion of the J-integral concept

is fulfilled.

In [6], the relationship between the fracture mechanical parameters determined according to the J-integral and the CTOD concept is considered using the example of the temperature dependence of the toughness of unoriented and cold-rolled oriented polypropylene ( abbreviation: PP). For the constraint factor, m = 0.7 is given for the examined PP material [7].

See also

• Fracture mechanics
• Fracture types
• Crack tip opening displacement concept (CTOD)

References

[1]	Cherepanov, G. P.: On Crack Propagation in Continuous Media. Applied Mechanics and Mathematics 31 (1967) 503
[2]	Rice, J. R.: A Path Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks. J. Appl. Mech. (1968) 379–386
[3]	Grellmann, W., Seidler, S. (Eds.):Polymer Testing. Carl Hanser Verlag, Munich (2022) 3. Edition, p. 239–241 (ISBN 978-1-56990-806-8; E-Book ISBN: 878-1-56990-807-5; see AMK-Library under A 23)
[4]	Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1993) 3. Auflage, (ISBN 3-342-00659-5; siehe AMK-Library under E 29-3)
[5]	Anderson, T. L.: Fracture Mechanics. Fundamentals and Applications. 2nd Ed., CRC Press, Boca Raton (1995) 2. Auflage, (ISBN 978-0849342608; siehe AMK-Library under E 8-1), DOI: [1]
[6]	Grellmann, W., Che, M.: Assessment of Temperature-dependent Fracture Behaviour with Different Fracture Mechanics Concepts on Example of Unoriented and Cold-rolled Polypropylene. J. Applied Polymer Science 66 (1997) 1237–1249; https://doi.org/10.1002/(SICI)1097-4628(19971114)66:7%3C1237::AID-APP4%3E3.0.CO;2-H
[7]	Hille, E.: Untersuchungen zum Bruchverhalten des orientierten isotaktischen Polypropylen. Ph.D. Dissertation, Technische Hochschule Leuna-Merseburg (1983)