SUMPTER and TURNER – J-Integral Estimation Method

Sprachauswahl/Language selection

Dieser Artikel ist auch auf Deutsch verfügbar Auswertemethode nach Sumpter und Turner

A service provided by
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Our further education offers: https://www.psm-merseburg.de/weiterbildung
PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

J-integral estimation method according to SUMPTER and TURNER (ST)

Basic assumption

J-integral estimation methods are used for the determination of fracture-mechanical characteristic values according to the J-integral concept.

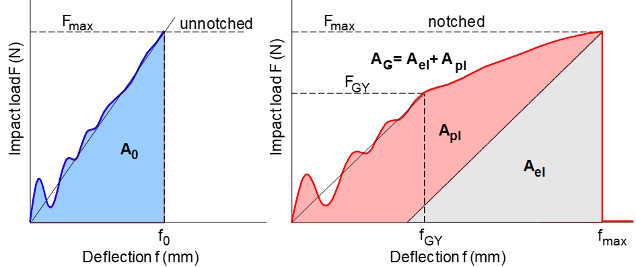
Sumpter and Turner [1] proposed to determine J_I^ST values by splitting the total energy A_G introduced by the external force into two parts, i.e., an elastic A_el and a plastic A_pl part with:

A_G = A_el + A_pl

Fig. 1:

Determination of J-integral according to Sumpter and Turner [1, 2]

Determination equation for SENB and CT specimen

The determination of J_I^ST values is then given by the following equation:

$J_{I}^{ST}=\eta _{el}{\frac {A_{el}}{B(W-a)}}+\eta _{pl}{\frac {A_{pl}}{B(W-a)}}\cdot ({\frac {W-a_{eff}}{W-a}})$

valid for 0 < a/W < 1

f(a/W) = 2 für a/w > 0.45

with:

Ael		elastic part of the deformation energy
Apl		plastic part of the deformation energy
ηel		elastic factor
ηpl		plastic factor and
ηel, ηpl		= f(a/W)

η_el can be determined from the elastic part of the load–load point displacement curve

η_pl is for three-point bending test specimens for a/W > 0.2 η_pl = 2

η_pl is for compact tension specimens for a/W > 0,6 η_pl = 2 (see ASTM STP 700)

For SENB test specimens, the following relationship applies for η_el:

$\eta _{el}={\frac {2F_{Gy}s^{2}(W-a)}{f_{Gy}EBW^{3}}}f^{2}\left({\frac {a}{W}}\right)(1-\nu ^{2})$

with: f (a/W) as correction function

In the literature, Schwalbe [3] and Blumenauer [4] give the following correlation (table):

Table: Values for ηel for different test specimens and a/W ratios

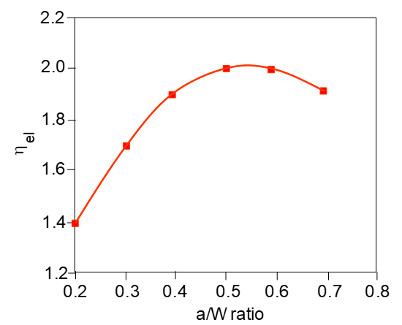
ηel	a/W	0.2	0.3	0.4	0.5	0.6	0.7
SENB	s/W = 4.0	1.4	1.7	1.9	2.0	2.0	1.9
CT	H/W = 1.2	3.7	2.7	2.4	2.3	2.2	2.2

Fig. 2:

Correlation between elastic factor and a/W-ratio [5, 6]

η_el is defined for the SENB test specimen as follows:

η_el = 5 (a/W)² + 5.5 (a/W) + 0.5

J_pl can also be determined using the COD test technique, but then requires knowledge of the rotation factor n:

$\eta _{pl}=2-{\frac {\left(1-{\frac {a}{W}}\right)(0.892)-4.476{\frac {a}{W}}}{1.125+0.892{\frac {a}{W}}-2.238\left({\frac {a}{W}}\right)^{2}}}$

Evaluation procedure

The experimental procedure for determining geometry-independent fracture-mechanical characteristic values with the aid of the instrumented Charpy impact test (ICIT) under dynamic loading is explained in detail in the validated procedure of the testing laboratory "Mechanical Testing of Plastics": MPK procedure "MPK-ICIT" [7].

See also

• J-integral concept
• J-Integral evaluation method (overview)
• J-integral estimation methods of

- RICE, PARIS and MERKLE

- MERKLE and CORTEN (MC)

- BEGLEY and LANDES

- KANAZAWA

References

[1]	Sumpter, J. D. G., Turner, C. E.: ASTM STP 601 (1976): Cracks and Fracture. Method for Laboratory Determination of Jc. p. 3–18
[2]	Grellmann, W., Seidler, S. (Eds.): Polymer Testing. Carl Hanser, Munich (2022) 3. Edition, 251–253, (ISBN 978-1-56990-806-8; e-book 978-1-56990-807-5) (see AMK-Library under A 22)
[3]	Schwalbe, K.-H.: Bruchmechanik metallischer Werkstoffe. Carl Hanser Verlag, München Wien (1980), (ISBN 3-446-12983-9; siehe AMK-Library under E 15)
[4]	Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (2003) 3rd Edition (see AMK-Library under E 29-3)
[5]	Sumpter, J. D. G.: Elastic-Plastic Fracture Analysis and Design Using the Finite Element Method. Ph.D thesis University of London (1974)
[6]	Chipperfield, C. G.: A Summary and Comparison of J Estimation Procedure. Journal of Testing and Evaluation (JTEVA), Vol. 6 No. 4 July (1978) 253–259 (https://doi.org/10.1520/JTE10951J)
[7]	MPK procedure "MPK-ICIT" (2016-03): Testing of Plastics – Instrumented Charpy Impact Test (ICIT): Procedure for Determining the Crack Resistance Behaviour Using the Instrumented Impact Test; Part I: Determination of Characteristic Fracture Mechanics Parameters for Resistance Against Unstable Crack Propagation; Part II: Determination of Characteristic Fracture Mechanics Parameters for Resistance Against Stable Crack Propagation