ICIT – Nonlinear Material Behaviour

Sprachauswahl/Language selection

Dieser Artikel ist auch auf Deutsch verfügbar IKBV Nichtlineares Werkstoffverhalten

A service provided by
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Our further education offers: https://www.psm-merseburg.de/weiterbildung
PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

ICIT – Nonlinear material behaviour

Determination of impact load F_GY and deflection f_GY for elastic–plastic material behaviour

The dominant evaluation method problem of the instrumented Charpy impact test in determining fracture mechanical material parameters from impact load (F)–deflection (f) diagrams with nonlinear material behaviour lies in the determination of the force F_GY at the transition from elastic to elastic–plastic material behaviour and the associated deflection f_GY [1, 2].

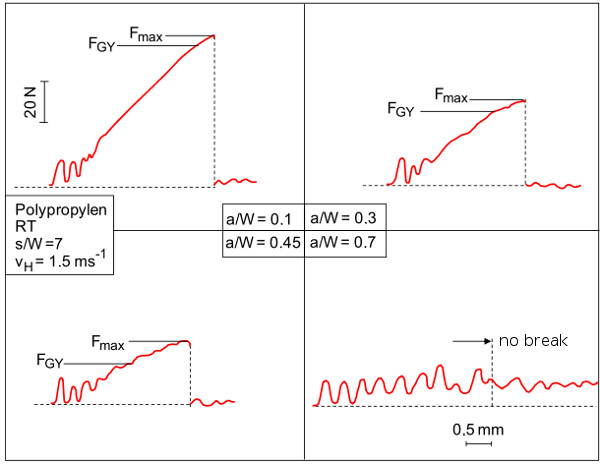
Typical impact load‒deflection diagrams for polypropylene (PP)

The problem of determining the measured variables from the F–f diagram will be explained using the example of investigations into the dependence on the a/W ratio for a polypropylene (abbreviation: PP) material at room temperature.

Fig. 1:

Typical impact load (F)–deflection (f) diagrams for polypropylene (abbreviation: PP) at different a/W ratios

Figure 1 shows typical F–f diagrams for the various a/W ratios 0.1, 0.3, 0.45, and 0.7 (see also: ICIT – types of impact load–deflection diagrams).

The F–f diagrams shown indicate that

1. the relationship between impact load and specimen deflection becomes increasingly nonlinear as the a/W ratio increases
2. the maximum impact load F_max decreases as the a/W ratio increases, and
3. the amplitude of the inertial load F₁ remains approximately constant.

For a/W > 0.7, the forces F_max and F_GY become so small in comparison to the superimposed oscillation that the condition F_max > F₁ (see also: ICIT – experimental conditions) can no longer be fulfilled and it is not possible to determine them meaningfully in the recording diagram.

Results for selected plastics

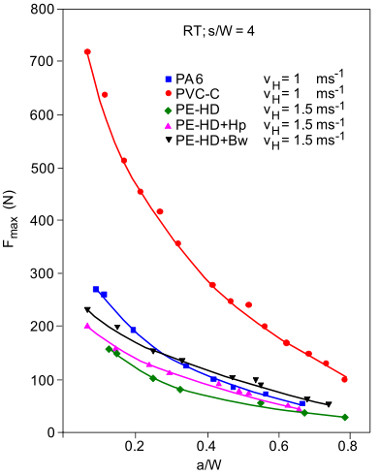
Analogous results were also obtained in [1] for a post-chlorinated PVC material (abbreviation: PVC-C) [3, 4], two polyamide (abbreviation: PA) materials [4, 5], a high-density polyethylene (abbreviation: PE-HD) [5], on PE-HD filled with cotton (BW) and on PE-HD filled with hard paper (HP) [6].

Figure 2 shows the decrease in maximum impact load F_max with increasing a/W ratio, i.e., smaller residual cross-section for these materials.

Fig. 2:

Dependence of the maximum impact load Fmax on the a/W ratio for selected plastics

In order to generate suitable F–f diagrams for the evaluation, the demand for the use of a low a/W ratio is derived from the results presented, whereby the evaluability of the diagrams must be ensured by complying with the control condition explained under “ICIT – experimental conditions” with regard to the inertial load, the fracture time and the energy consumption.

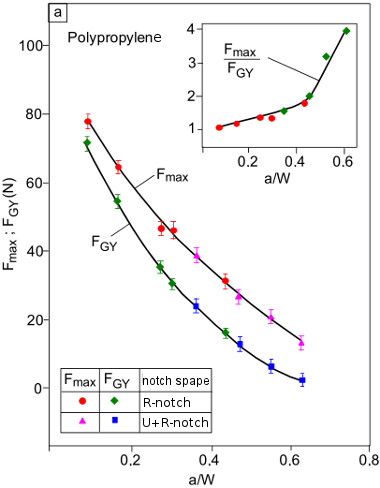
This requirement is in contrast to the requirements set out in various standards, e.g. in [7], according to which the a/W ratio should be 0.35 ≤ a/W ≤ 0.55 for application according to the concept of linear-elastic fracture mechanics (LEBM) (see also: fracture mechanics) or the equivalent energy concept. The loads F_max and F_GY determined from the F–f diagrams decrease with the decrease in the residual cross-section B(W-a) for the materials investigated, as shown in Fig. 3.

Fig. 3:

Dependence of the loads Fmax, FGY (a) and the corresponding deflections fmax, fGY (b) for polypropylene (abbreviation: PP) on the a/W ratio

Evaluation of the non-linearity of material behaviour

Information about the non-linearity is provided by the ratio F_max/F_GY, which is plotted in the partial image in Fig. 3 as a function of the a/W ratio. For F_max/F_GY = 1, linear-elastic fracture mechanics (LEFM) must be applied and for F_max/F_GY > 1, elastic–plastic fracture mechanics (EPFM) must be applied. Not unproblematic in its interpretation is the course of the deflection with increasing a/W ratio, which, in addition to the problem of the bending of the notched test specimen with large deflections and the change in the notch factor αK with the notch geometry, also contains the additional possible effect of the “pulling through” of the test specimens through the abutments, at least for large support distance [1]. If the ratio of the deflections f_max/f_GY is taken as a measure of the non-linearity, it can be seen that this increase is a sensitive indicator of the non-linearity and allows a statement to be made about the fracture mechanics concept to be applied.

Assuming [1, 8] that the experimentally measured specimen deflection f_max is calculated of the unnotched part f_B and the part f_K caused by the deformation in the area of the notch according to

$f_{max}=f_{k}+f_{B}$

(1)

whereby the bending component is determined via the relationship

$f_{B}={\frac {F_{max}\cdot s^{3}}{4BW^{3}E}}$

(2)

with E = modulus of elasticity in the bending test, the relationship shown in Fig. 3 can be interpreted (see also: extended CTOD concept).

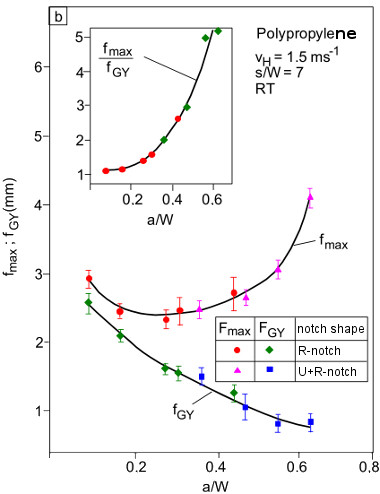
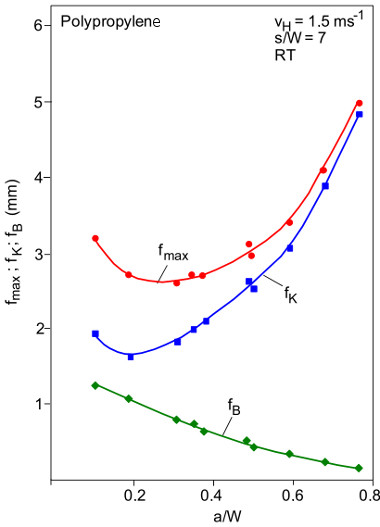
Figure 4 shows the individual parts according to equation (1) as a function of the a/W ratio using the example of a polypropylene material (abbreviation: PP).

Fig. 4:

Deflection parts fmax, fK and fB at the beginning of unstable crack growth for polypropylene (abbreviation: PP)

Figure 4 shows that the bending component decreases with increasing a/W ratio, i.e. at a/W = 0.1 it accounts for 40 % of the total deflection and at a/W = 0.7 only 5 %. For high notch depths, the part f_K dominates.

In [1] it is shown for materials with higher elastic proportions of the total deformation, such as selected PA materials and PVC-C, that the bending proportion is considerably higher in this case.

See also

• Fracture mechanics
• Deformation
• ICIT – experimental conditions
• Instrumented Charpy impact test
• Viscoelastic material behaviour

References

[1]	Grellmann, W.: Beurteilung der Zähigkeitseigenschaften von Polymerwerkstoffen durch bruchmechanische Kennwerte. Habilitation (1986), Technischen Hochschule Merseburg, Wiss. Zeitschrift TH Merseburg 28 (1986), H. 6, pp. 787–788 (Content, Summary)
[2]	Server, W. L.: Impact Three-point Bend Testing for Notched and Precracked Specimens. Journal of Testing and Evaluations JTEVA, 6 (1978) 1, 29–34
[3]	Hoffmann, H., Grellmann, W.: Zur Bestimmung der dynamischen Bruchzähigkeit von Polymerwerkstoffen im instrumentierten Kerbschlagbiegeversuch. Plaste und Kautschuk 30 (1983) Publ. Nr. 14 H. 6, 324‒330 (Download as pdf)
[4]	Hoffmann, H., Grellmann, W., Zilvar, V. Sommer, J. P., Michel, B.: Anwendung verschiedener J-Integral-Näherungsverfahren zur Beschreibung der Zähigkeitseigenschaften von Polymerwerkstoffen. Wiss. Zeitschrift der THLM 28 (1986) H 1, 58‒67
[5]	Eve, S.: Untersuchungen zum Einfluss der Kerbtiefe und der Hammergeschwindigkeit auf die dynamische Bruchzähigkeit mit Hilfe des instrumentierten Kerbschlagbiegeversuches. Ingenieurbeleg TH Leuna-Merseburg, 1983 (siehe AMK-Library unter B 3-15)
[6]	Seidler, S.: Kerbschlagbiegeverhalten von gefüllten und verstärkten Polymerwerkstoffen. Ingenieurbeleg, TH Leuna-Merseburg 1983 (see AMK-Library under B 2-14)
[7]	ASTM E 399 (2024): Standard Test Method for Linear-Elastic Plane-Strain Fracture Toughness of Metallic Materials, Annual Book of ASTM Standards; DOI: 10.1520/E0399-24
[8]	Srawley, J. E.: On the Relation of JI to Work Done per Unit Incracked Area: 'Total', or Component "Due to Crack". Intern. Journal of Fracture Mechanics 12 (1976) 470‒474; https://link.springer.com/article/10.1007/BF00032843#citeas