Crack Model according to BARENBLATT

Sprachauswahl/Language selection

Dieser Artikel ist auch auf Deutsch verfügbar

A service provided by

Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Our further education offers: https://www.psm-merseburg.de/weiterbildung
PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Crack model BARENBLATT

Fundamentals of the model

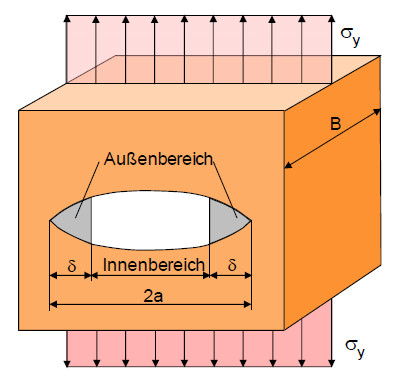
The GRIFFTITH and IRWIN & MC CLINTOCK crack models have in common that infinitely large stresses occur at the crack tip with a very sharp notch. In order to eliminate this discrepancy between the model conceptions and the practically possible conditions, BARENBLATT developed a model for the elasticity-theoretical description of the stress conditions at the crack tip. The crack is divided into an inner and two outer areas.

Fig. 1:

Crack model according to BARENBLATT

In BARENBLATT's crack model, atomic or molecular cohesive forces are assumed, which lead to a smooth closing of the crack surfaces.

The crack opens continuously in the outer area δ, the interpretation is that the atomic and molecular distances in the area δ increase continuously and an interaction takes place in the form of cohesive forces. These can reach the theoretical strength of the material. (Cohesion: Cohesion of the molecules of a body)

Cohesive forces and cohesive modul

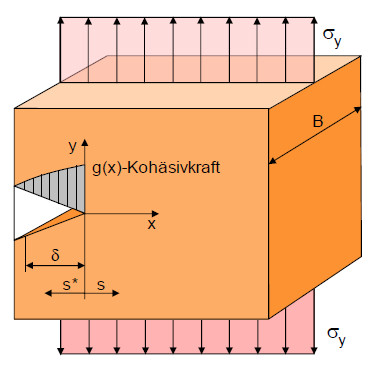
Figure 2 shows the course of the cohesive forces and the resulting stresses in the x-direction over the crack length.

Fig. 2:

Stress distribution at the crack tip according to BARENBLATT

BARENBLATT formulated the integral of the distribution of the cohesive forces over the crack cross-section as a material parameter and called it the cohesive modulus

B=\int _{0}^{\delta }{\frac {g(s^{*})ds^{*}}{\sqrt {s^{*}}}}

oder:

B=\int _{0}^{\delta }{\frac {g(x)}{\sqrt {x}}}dx

with

s^* –		coordinate in x-direction
g –		cohesive force

Although a number of methods for calculating the cohesive modulus have been proposed, an exact determination of this characteristic material parameter remains problematic.

The advantage of BARENBLATT's crack model is that the infinitely large stress values occurring at the crack tip in GRIFFITH's crack model are avoided, and possible distributions of the stress at an infinitely sharp crack are described.

In recent years, however, there has been an increased interest in this crack model, also known as the cohesive zone model. This is also due, apart from the extension of the model itself, to the immense progress in computer technology.

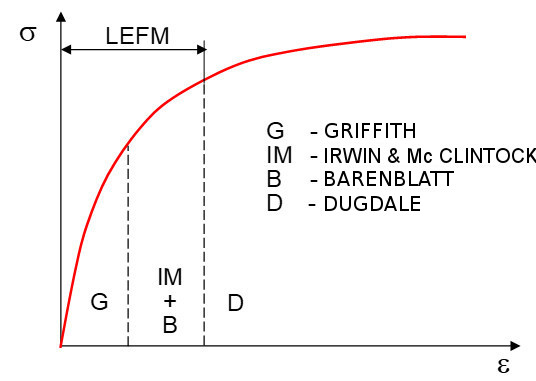
Application area

Fig. 3:

Valid ranges of crack models

Importance of the model

This theory had relatively little application in practice for a long time. There are examples of application in the analysis of:

geological fracture processes
stress corrosion cracking of polymers
crack propagation at interfaces / in boundary layers (interlaminar crack propagation, crack propagation in adhesive and welded joints etc.)

Fundamentals of the model

Cohesive forces and cohesive modul

Application area

Importance of the model

See also