Crack Model according to IRWIN and Mc CLINTOCK

Sprachauswahl/Language selection

Dieser Artikel ist auch auf Deutsch verfügbar Rissmodell nach IRWIN und Mc CLINTOCK

A service provided by
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Our further education offers: https://www.psm-merseburg.de/weiterbildung
PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Crack model to IRWIN & Mc CLINTOCK

Basics of the model

The application of the crack model according to GRIFFITH and the determination of the fracture toughness values based on it are linked to a purely elastic deformation of the stressed material.

However, most technical materials exhibit plastic deformation in the microscopic range even when a macroscopically brittle fracture occurs.

In order to ensure the applicability of linear elastic fracture mechanics (LEFM), the plastic deformations at the crack tip must be small in comparison to the crack length and the component dimensions.

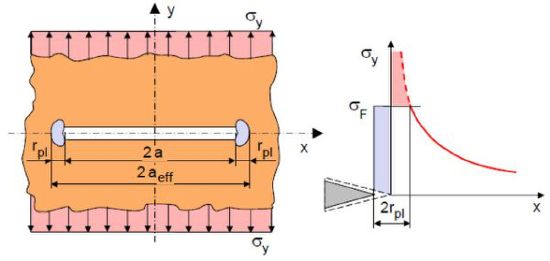
Fig. 1:

Crack model according to Irwin and Mc Clintock

According to the model established by Irwin and Mc Clintock [1–3], it is assumed that the crack length required to calculate the fracture toughness is composed of the initial crack length a₀ and the radius of the plastic zone a_pl as the effective value a_eff (for experimental determination see effective crack length).

$a_{eff}=a_{0}+a_{pl}$

Linear-elastic fracture mechanics with small-scale yields

The fracture mechanics concept based on this is explained under the basic term fracture mechanics and is referred to as linear-elastic fracture mechanics with small-scale yields.

The size of the plastic zone a_pl can be estimated simply by replacing the stress components in the SNEDDON-WILLIAMS equations with the yield strength R_e (R_e = σ_F).

For Θ = 0 you get:

$r_{pl}=a_{pl}={\frac {1}{2\pi }}({\frac {K_{I}}{R_{e}}})^{2}$

for [[[Plain Stress and Strain State|plain stress state]] and

$r_{pl}=a_{pl}={\frac {1}{2\pi }}({\frac {K_{I}}{R_{e}}})^{2}(1-2\upsilon )^{2}$

für den [[[Plain Stress and Strain State|plain strain state]].

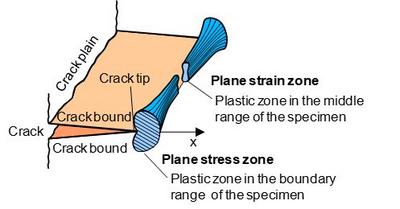
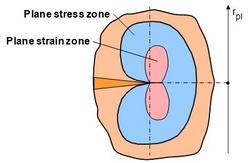
Due to the increasing deformation constraint towards the centre of the specimen, the plane stress state prevailing at the edge of the specimen changes to the plane strain state. The plastic zone is smaller in the centre of the specimen, resulting in the formation of the so-called ‘dog bone model’

Fig. 2:

Plastic zone in front of the crack tip along the specimen width

Fig. 3:

Form of the plastic zone in front of the crack tip along the specimen width

In this case, the stress intensity factor is calculated as follows

$K_{I}=\sigma (\pi a_{eff})^{\frac {1}{2}}f(a_{eff}/W)$

The application of this model is limited to the case of

${\frac {R_{m}}{R_{e}}}\leq 0.6$

Ratio of tensile strength to yield stress

If this condition is not met and larger plastically deformed areas occur, then the methods of yield fracture mechanics must be applied. Three-dimensional FEM calculations taking into account the hardening behaviour have shown that the actual shape deviates from these model concepts.

Formation of the plastic zone for plastics

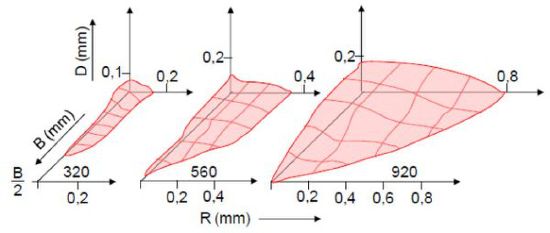
As the experimental verification is very complex, there are only a few findings in the literature [4].

Figure 4 shows an example of a plastic zone in an isotactic polypropylene ( abbreviation: PP)

Fig. 4:

Example: Plastic zone in a polypropylene material [4]

The most important applications of an appropriate corrected application of fracture mechanics to plastics today lie in the question of the structure-related realisation of the plastic zone. An answer to this question naturally depends on the specific microstructure of the plastic.

See also

• Fracture mechanics
• Crack models
• Crack model according to BARENBLATT
• Crack model according to GRIFFITH
• Crack model according to DUGDALE

References

[1]	Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1982) p. 20 (see AMK-Library under E 29-1)
[2]	Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig (1987) 2nd Edition, p. 20 (ISBN 3-342-00096-1; see AMK-Library under E 29-2)
[3]	Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1993) 3rd Edition, p. 17 (ISBN 3-342-00659-5; see AMK-Library under E 29-3)
[4]	Hoffmann, H., Grellmann, W., Hille, E., Newe, R.: Ermittlung und Anwendung bruchmechanischer Kennwerte zur Beschreibung der Zähigkeitseigenschaften von isotaktischem Polypropylen. Plaste und Kautschuk 29 (1982), H. 4, p. 230–237) (Download as pdf)