Geometry Criterion

Sprachauswahl/Language selection

Dieser Artikel ist auch auf Deutsch verfügbar Geometriekriterium

A service provided by
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Our further education offers: https://www.psm-merseburg.de/weiterbildung
PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Geometry criterion

Geometry criterion, fracture tougness

In the linear-elastic approach, the geometric variables B, a and the ligament expansion (W–a) are estimated using the empirically determined relationship

$B{,}\ a{,}\ \left(W-a\right)\,\geq \,\beta \left({\frac {K}{\sigma _{y}}}\right)^{2}$

with

$\sigma$ y

Yield stress (yield point).

The geometry constant $\beta$ is material-dependent.

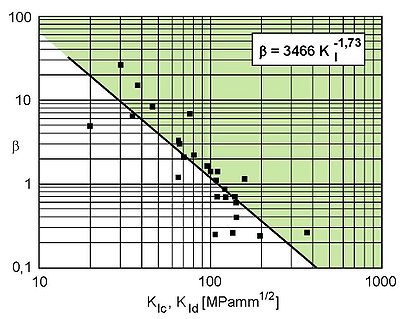
Experimental results regarding the influence of the test specimen thickness B on the fracture mechanical properties (see: fracture mechanical testing) for plastics are available in the literature. Figure 1 shows the dependence of the coefficient according to the above equation on the fracture toughness determined under quasi-static and impact loading (see: impact loading of plastics) for various plastics. The relationship shown was established on the basis of experimentally determined thickness and a/W dependencies and has a high degree of generalisation, as a common relationship results regardless of the type of stress (quasi-static, impact) and the material failure (stable, unstable) (see: Crack propagation).

Fig. 1:

Dependence of the coefficient $\beta$ on the fracture toughness KIc, KId for different plastics

References

• Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1993) (ISBN 3-342-00659-5; see AMK-Library under E 29-3)
• Anderson, T. L.: Fracture Mechanics. Fundamentals and Applications. 3rd Ed., CRC Press, Boca Raton (2005) (ISBN 978-0849342608; see AMK-Library under E 8-2), DOI: https://doi.org/10.1201/9781315370293
• Grellmann, W., Seidler, S., Lach, R.: Geometrieunabhängige bruchmechanische Werkstoffkenngrößen – Voraussetzung für die Zähigkeitscharakterisierung von Kunststoffen. Materialwissenschaften und Werkstofftechnik 32 (2001) 552–561, https://doi.org/10.1002/1521-4052(200106)32:6%3C552::AID-MAWE552%3E3.0.CO;2-O
• Akay, M.: Fracture Mechanics Properties. In: Brown, R. P. (Ed.): Handbook of Polymer Testing. Marcel Dekker Inc., New York (1999) 533–588 (ISBN 978-0824701710; see AMK-Library under C 5)

Geometry criterion, J-integral concept

Due to the elastic-plastic material behaviour typical of plastics, especially with decreasing test specimen thickness, decreasing stress velocity and increasing temperature, and the limits for the applicability of linear-elastic fracture mechanics, it is necessary to use the J-integral concept to describe the geometry dependence. The critical J-values are geometry-independent if the criterion

$B{,}\ a{,}\ \left(W-a\right)\,\geq \,\varepsilon {\frac {J}{\sigma _{y}}}$

with

$\varepsilon$

material-dependent constant of the geometry criterion of the J-integral concept

is fulfilled.

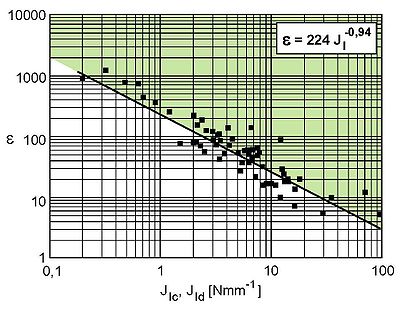
For the geometry constant from this criterion, Figure 2 shows a tendency to decrease with increasing toughness, which $\varepsilon$, like the geometry constant $\beta$, must be regarded as a material-dependent variable and can assume values between 5 and 1220, which represent maximum values for impact loading.

Fig. 2:

Dependence of the coefficients $\varepsilon$ on the J-value for different plastics

Knowledge of the general $\varepsilon$-J relationship allows the required test specimen thicknesses to be estimated. The advantage of determining fracture mechanics values under impact loading lies in the possibility of obtaining geometry-independent values even at low test specimen thicknesses.

References

• Grellmann, W., Seidler, S., Lach, R.: Geometrieunabhängige bruchmechanische Werkstoffkenngrößen – Voraussetzung für die Zähigkeitscharakterisierung von Kunststoffen. Materialwissenschaften und Werkstofftechnik 32 (2001) 552–561
• Grellmann, W.: New Developments in Toughness Evaluation of Polymers and Compounds by Fracture Mechanics. In: Grellmann, W., Seidler, S.: Deformation and Fracture Behaviour of Polymers. Springer Berlin Heidelberg (2001) p. 3–26, (ISBN 3-540-41247-6; see AMK-Library under A 7)

Geometry criterion, crack opening displacement

The requirements for the test specimen geometry are estimated using the Crack tip opening displacement concept

$B{,}\ a{,}\ \left(W-a\right)\,\geq \,\xi \cdot \delta$.

with

$\xi$

material-dependent constant of the geometry criterion of the CTOD concept

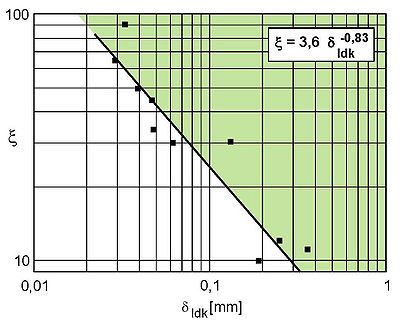
Fig. 3:

Dependence of the coefficient $\xi$ on the critical crack opening $\delta$Idk

In addition to the J-integral concept, the CTOD concept is used in particular to describe deformation-determined fracture processes. The prerequisite for determining critical crack openings is the formation of a quasi-static stress state. On the basis of the “Plastic Hinge Model”, the critical crack opening is determined for impact-type loading, which is independent of the a/W ratio at B = 4 mm for a/W > 0.2. Figure 3 shows that $\xi$-values between 10 and 90 can be assumed and that a considerable overestimation of the required minimum test specimen dimensions is possible if the necessary notch depth or test specimen thickness is still unknown.

See also

• Fracture mechanics
• Crack models
• J-integral concept
• Crack tip opening displacement concept (CTOD)

References

• Grellmann, W., Seidler, S.: Determination of Geometry Independent Fracture Mechanics Values of Polymers. Int. J. of Fracture 68 (1994) R19–R22, https://doi.org/10.1007/BF00032333
• Grellmann, W., Seidler, S., Hesse, W.: Procedure for Determining the Crack Resistance Behaviour Using the Instrumented Charpy Impact Test. In: Grellmann, W., Seidler, S.: Deformation and Fracture Behaviour of Polymers. Springer Berlin Heidelberg (2001) S. 71–86, (ISBN 3-540-41247-6; AMK-Library under A 7)