Flexural Modulus

Sprachauswahl/Language selection

Dieser Artikel ist auch auf Deutsch verfügbar Biegemodul

A service provided by
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Our further education offers: https://www.psm-merseburg.de/weiterbildung
PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Flexural modulus

Determination methods

The flexural modulus E_f is usually determined in a three-point or four-point bending test under quasi-static loading [1–3] on plastics or short-fibre reinforced or filled plastic composites. The test on rigid and semi-rigid plastics, i.e. thermoplastic moulding compounds or extrusion and casting compounds, is carried out in accordance with ISO 178 [2] in a three-point bending test.

For fibre-reinforced plastics, the three-point or four-point bending test (method A or B) according to ISO 14125 [3] can be used. However, the flexural modulus can also be determined as a complex modulus under dynamic loading (see: dynamic-mechanical analysis (DMA) – bend loading).

Definition of the flexural modulus

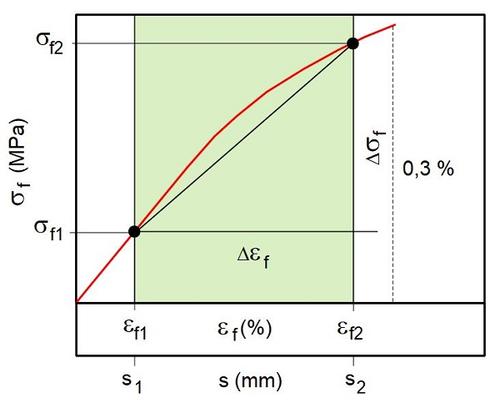
The determination of the modulus of elasticity under quasi-static bend loading in polymer testing does not differ in principle from other mechanical stress, such as in tensile testing or compression testing. The modulus of elasticity is determined in the linear elastic and linear-viscoelastic deformation range as the secant modulus between 0.05 and 0.25 % peripheral fibre strain (see also: elastic modulus – examples and material values), whereby the test speed can be identical to that of the actual bending test (Fig. 1). In analogy to the tensile test, however, different test speeds can also be used to determine the modulus of elasticity and the bending properties, whereby the switchover point of the test speeds must then be above 0.25 % peripheral fibre strain. The general calculation of the flexural modulus E_f is carried out according to Eq. (1), but in the specific metrological case, the geometric conditions and the measurement location must be taken into account.

$E_{f}={\frac {\sigma _{f2}-\sigma _{f1}}{\varepsilon _{f2}-\varepsilon _{f1}}}={\frac {\Delta \sigma _{f}}{\Delta \varepsilon _{f}}}={\frac {\Delta \sigma _{f}}{0,002}}$

(1)

Fig. 1:

Determination of the secant modulus in three-point and four-point bend tests

Metrological Determination of the flexural modulus

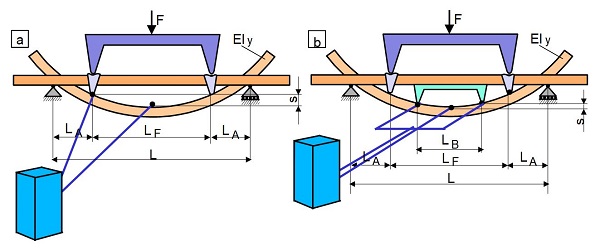
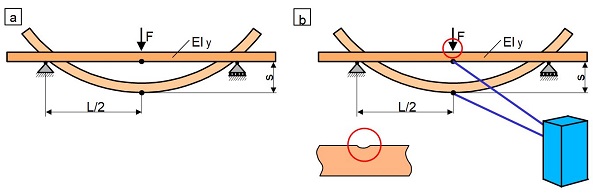
To determine the flexural modulus E_f, the quasi-static polymer testing under flexural stress of the three-point or four-point flexural test is used with a material testing machine. When applying the ISO 178 standard, only the three-point flexural test is specified, whereby the measurement of the centre deflection is generally used here. In the case of the bending test, the traverse path measurement (Fig. 2a) can be used to determine the centre deflection (Eq. 2), whereas a centrally positioned extensometer must be used to determine the flexural modulus (Fig. 2b). In this equation, I_y is the minimum axial moment of inertia (see: bend test) of the prismatic test specimen.

$s={\frac {F\cdot L^{3}}{48\cdot E_{f}\cdot I_{y}}}$

(2)

Since the reference point for the deflection measurement is identical for both the traverse path measurement (see also: tensile test and compression test) and when using a centre sensor (support of the bending fins), the calculation Eq. (3) is the same for both measurement cases.

$E_{f}={\frac {F\cdot L^{3}}{s\cdot 4b\cdot h^{3}}}$

(3)

Fig. 2:

Determination of the flexural modulus in a three-point bending test: (a) by measuring the traverse path and (b) using a extensometer

The advantage of the extensometer lies in the fact that the penetration of the bending fin into the surface of the test specimen is not recorded, which means that the bending modulus is slightly higher (up to approx. 10 %) compared to traverse path measurement. Such bending sensors are commercially available from ZwickRoell GmbH & Co. KG, Ulm, and formerly Instron Deutschland GmbH, Pfungstadt (Fig. 3).

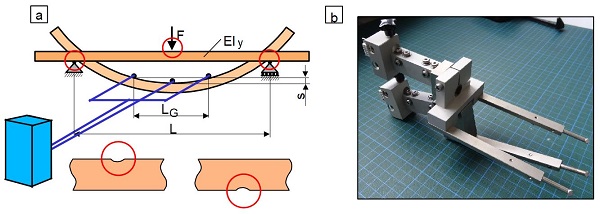
In conjunction with the Multisens transducer from ZwickRoell, adapters for use in compression tests and bending tests are also available in addition to the extensometers for tensile tests (see: tensile test, path measurement technique). The central sensor can be used to measure the compressive modulus, but also to record the centre deflection for determining the flexural modulus in three- and four-point bending tests (see: Fig. 2b). If the penetration of the supports in the bending test is not to be recorded in the measurement signal, so-called fork sensors can be used as an alternative, which generate a differential measurement signal between the forks and the central sensor. Due to the fact that this measurement signal is significantly smaller than, for example, the traverse path, high-resolution measurement techniques must be used here (Fig. 4).

Fig. 3:

Extensometer for mid-span deflection (a) Deflectometer W-E401-H from Fa. Instron Deutschland GmbH, Pfungstadt, and (b) bending sensor BTC-EXOMFL.H01 from Fa. ZwickRoell GmbH & Co. KG, Ulm

Fig. 4:

Application of (a) fork gauges in three-point bending tests and (b) fork gauges for the Multisens transducer from Fa. ZwickRoell GmbH & Co. KG, Ulm

The deflection depends on the geometric dimensions of the fork sensor and is calculated according to Eq. (4). The calculation of the flexural modulus using fork sensors, which is often not included in the test software of the test machine manufacturer, can be programmed and evaluated using external software according to Eq. (5).

$s={\frac {F\cdot L_{G}^{2}}{96\cdot E_{f}\cdot I_{y}}}\cdot (3L-L_{G})$

(4)

$E_{f}={\frac {F\cdot L_{G}^{2}(3L-L_{G})}{s\cdot 8b\cdot h^{3}}}$

(5)

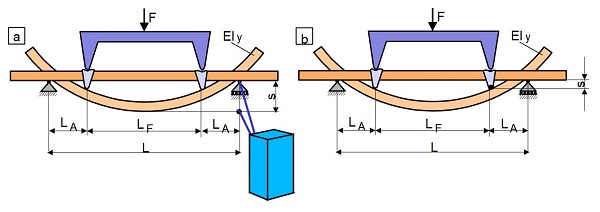
When determining the flexural modulus in the four-point bending test, there are various measurement variants that place different demands on the measurement technology. The simplest options here are also to use the traverse path (Fig. 5a) and to measure the centre deflection in analogy to the three-point bending test (Fig. 5b).

Fig. 5:

Application of (a) mid-span deflection in four-point bending test and (b) traverse path measurement

In the case of four-point bending, the bending modulus is obtained from the relative movement between the supports (see: support distance) and an extensometer attached centrally, using the mid-span deflection s (Fig. 5a) according to Eq. (6).

$E_{f}={\frac {F\cdot L_{A}}{s\cdot 4b\cdot h^{3}}}\left[4L_{A}(3L_{F}+2L_{A})+3L_{F}^{2}\right]$

(6)

With the traverse path s (Fig. 5b), in the case of four-point bending, the bending modulus is calculated as the path difference between the fixed bending beam and the supports according to Eq. (7).

$E_{f}={\frac {F\cdot L_{A}^{2}}{s\cdot b\cdot h^{3}}}\left(3L_{F}+2L_{A}\right)$

(7)

Fig. 6:

Application of (a) fork gauges in three-point bending tests and (b) Multisens fork gauges from ZwickRoell

The flexural modulus is calculated here from the difference s between the centre of the reference or flexural beam and the traverse movement according to Fig. 6a using Eq. (8), thereby avoiding influences on the deflection due to HERTZIAN pressure and penetration at the supports.

$E_{f}={\frac {3F\cdot L_{F}^{2}\cdot L_{A}}{s\cdot 4b\cdot h^{3}}}$

(8)

The relative distance s between the centre of the reference beam system or loosely mounted fork sensors and the centre of the test specimen within the bending beam gives the bending modulus according to Fig. 6b and Eq. (9). With this type of measuring system, influences on the deflection due to pressure on the supports and the test stamp can be avoided, although this requires a high-resolution measuring system.

Characteristic values of the three-point bending test

A comprehensive literature analysis of flexural moduli and flexural strengths for numerous plastics is contained in [4], from which the characteristic values for selected materials are shown in Table 1. Due to the importance of the materials, only unreinforced plastics and plastics with a 30 M.-% filler or reinforcement content were included in this list, which were generally determined by measuring the traverse path at room temperature.

Table 1: Characteristic values of the bend test for technical plastics according to [4]

material groupe	modification	Ef (MPa)	σfM (MPa)
ABS		1373 – 3792	47.1 – 95.1
	ABS + 30 M.-% GF	6067 – 9400	86.9 – 162
	ABS + 30 M.-% CF	16547	179
	ABS / PBT + 30 M.-% GF	8205 – 10100	147 – 186
	ABS / PC + 30 M.-% GF	7505 – 8136	137 – 167
ASA		1344 – 3000	38.6 – 84.8
PA 11	PA 11	300 – 1241	51.7 – 75.8
PA 12		345 – 2068	20.0 – 98.6
	PA 12 + 30 M.-% GF	5516 – 7100	150 – 185
PA 612		1724 – 2758	82.7 – 96.5
PA 6	PA 6 (normfeucht)	380 – 1400	75.8 – 127
	PA 6 + 30 M.-% GF (normfeucht)	2600 – 5600	192 – 200
	PA 6 + 30 M.-% GB (normfeucht)	1400 – 4482	100 – 138
	PA 6 + 30 M.-% MF (normfeucht)	4000 – 5396	98.1 – 124
	PA 6 + 30 M.-% CF (normfeucht)	14000 – 17237	310
PAEK		17000	130
PBI		6500	220
PBT		1900 – 2760	62.1 – 101
	PBT + 30 M.-% GF	6343 – 11500	150 – 225
	PBT + 30 M.-% MF	3500 – 4500	90.0 – 110
PC		1889 – 2786	71.7 – 114
	PC + 30 M.-% GF	6180 – 8900	147 – 220
	PC + 30 M.-% CF	15900 – 16200	207 – 241
PE-HD		689 – 1655	25.5 – 32.4
PE-LD		69.0 – 621	7.0 – 15.2
PE-LLD		207 – 827	-
PE-MD		345 – 900	-
PE-UHMW		276 – 923	41.4
PEEK		2758 – 4300	103 – 170
	PEEK + 30 M.-% GF	8963 – 12000	221 – 261
PEI		2900 – 3447	89.6 – 165
PEK		4200 - 6205	207
PET		1090 – 2758	79.3 – 82.7
	PET + 30 M.-% GF	6965 – 11928	123 – 240
PMMA		1200 – 3654	46.2 – 121
	PMMA + 30 M.-% GF	6481	106
POM		1471 – 3150	52,0 – 95,1
	POM + 30 M.-% GF	6890 – 9000	121
	POM + 30 M.-% GB	1900 – 3170	62.1
PP		1500 – 2462	-
	PP + 30 M.-% GF	4975 – 7001	136 – 157
	PP + 30 M.-% T	2340 – 3900	38.6 – 55.2
	PP + 30 M.-% MF	2300 – 3700	40.2 – 54.9
	PP + 30 M.-% GB	1290 – 1600	-
	PP + 30 M.-% CaCO3	1896 – 2800	32.4 – 45.0
PS		1724 – 3447	37.9 – 75.8
PVC		1810 – 3378	33.0 – 93.1
	PVC + 30 M.-% GF	7930 – 9310	145 – 159
PVDF		413 – 3309	48.3 – 94.1
	PVDF + 30 M.-% GF	6300	85.0
SAN		3447 – 3792	103 – 135
TPC		196 – 3330	66,2 – 71,7
TPO		83,0 – 1569	15.2 – 43.4
TPU		345 – 750	9.0 – 14.5
	TPU + 30 M.-% GF	2175	15.2
TPZ		689	6.2

GF: glass fibres, GB: glassballs, MF: mineral fibres, MX: unspecified mineral filling, GX: unspecified glass filling

See also

• Bend test
• Flexural strength
• Bend loading
• Elastic modulus
• Indentation modulus

References

[1]	Bierögel, C.: Bend Test on Polymers. In: Grellmann, W., Seidler, S. (Eds.): Polymer Testing. Carl Hanser Munich (2022) 3rd Edition, pp. 133–143 (ISBN 978-1-56990-806-8; see AMK-Library under A 22)
[2]	ISO 178 (2019-04): Plastics – Determination of Flexural Properties
[3]	ISO 14125 (1998-03): Fiber-reinforced Plastic Composites – Determination of Flexural Properties (ISO 14125 Technical Corrigendum 1: 2001-07; ISO 14125 AMD 1: 2011-02)
[4]	Bierögel, C., Grellmann, W.]: Bend Loading. In: Grellmann, W., Seidler, S.: Mechanical and Thermomechanical Properties of Polymers. Landolt-Börnstein. Volume VIII/6A3, Springer, Berlin (2014) pp. 164–191, (ISBN 978-3-642-55165-9; see AMK-Library under A 16)