Fatigue Crack Propagation Elastomers

Sprachauswahl/Language selection

Dieser Artikel ist auch auf Deutsch verfügbar Ermüdungsrissausbreitung Elastomere

A service provided by
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Our further education offers: https://www.psm-merseburg.de/weiterbildung
PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Fatigue crack propagation elastomers or crack growth curves elastomers

Measurement and testing requirements

The development and use of cyclic (dynamic) testing methods for elastomers is closely linked to the development of ‘Tear and Fatigue Analyses (TFA)’ by Bayer in collaboration with the company Coesfeld in 1992 [1, 2].

The performing of fracture mechanics tests under cyclic loading requires the availability of the appropriate testing technology and also specialised experience, as the experimental parameters, test specimen shape and size, twisting, mean stress and loading frequency and amplitude can be varied over a wide range. The influence of the test parameters on the crack growth curves determined was presented, for example, in the publications [3 ‒ 8].

With the use of a servo-hydraulic TA measuring system, it is possible to apply practical stresses, e.g. tyre loading, which is characterised by pulses, can be simulated well. For this reason, cyclic testing with TFA device systems is becoming increasingly popular, which can also be deduced from the increasing number of TFA devices in German-speaking countries. The TFA allows the simultaneous testing of up to 10 individual test specimens, whereby each loading and unloading cycle is recorded separately for each test specimen and automatic crack length detection is realised over the entire test period by determining the crack contour length using a CCD camera (Fig. 1) [9].

Fig. 1:

Tear Fatigue Analyser (TFA) of the company Coesfeld

Testing regime

The test specimens can be periodically loaded between a maximum and a minimum stress (stress-controlled) or strain (strain-controlled). During the experiment, various data such as temperature, ozone concentration, time, number of cycles and controlled systems are recorded, whereby the storage intervals can be freely selected. The force F, elastic and dissipated energy density W₀ and W_diss, deformation l, crack contour length a_eff and control path of the adjustment unit are recorded separately for each individual measuring station. A TFA test is therefore an economical way of generating measurement data to produce crack growth curves. In addition, the temperature in the test chamber can be varied between -50 °C and 150 °C and optionally also the climate in the test chamber. For example, testing under the influence of ozone is possible, which is of particular practical relevance for elastomers with unsaturated double bonds in the chain, such as NR, NBR or SBR. The TFA was originally designed for testing SENT-specimens, but recent studies [5, 8] have shown that the use of pure shear-specimens is preferable.

Crack growth curve of fracture mechanics

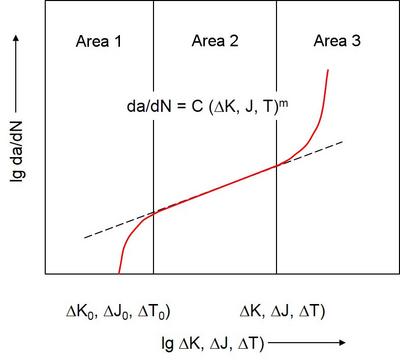
A schematic representation of a crack growth curve resulting from a cyclic fracture mechanics test is shown in Fig. 2. A crack growth curve is the double-logarithmic representation of the dependence of the crack growth rate on a fracture-mechanical toughness parameter such as K, J or, in the case of elastomer testing, T. The crack growth rate corresponds to the change in crack length ∆a as a function of the cycle length. The crack growth rate corresponds to the change in crack length Δa as a function of the number of cycles N and is usually given in the differential form da/dN. As can be seen from Fig. 2, two fracture mechanics parameters can be derived from such a crack growth curve: a threshold value and a critical value of the respective fracture mechanics parameter. In area 1, similar to area 3, there is a major influence of the microstructure, the mean stress and possible ambient media. For elastomers, the latter means that below the threshold crack energy T₀, crack propagation only occurs in the presence of ozone [10].

Fig. 2:

Crack growth curve according to [10, 11]

In the case of double-logarithmic plotting, area 2 is characterised by an almost linear relationship between the fracture-mechanical parameter and the crack growth rate, which can be described using the PARIS–ERDOGAN equation according to Eq. (1) [11, 12]:

${\frac {d\,a}{d\,N}}=C\cdot (\Delta K,\ \Delta J,\ \Delta T)^{m}$

(1)

with:
C, m – material-specific constants

If the load value increases above a critical value, area 2 changes to area 3, with a sharp increase in the crack propagation speed da/dN, i.e. a transition from stable crack propagation to accelerated stable or unstable crack propagation takes place here.

Crack growth curve of elastomers

Numerous studies [12–16] have shown that a large number of the elastomer materials analysed exhibit the theoretical crack growth curve shown in Fig. 2. The composition of the elastomers and therefore their structure also have an influence on crack growth behaviour, as do many physical properties. There are numerous studies in the literature that deal with the evaluation of fatigue crack behaviour in relation to the material composition. Papadopoulos et al. [17], for example, investigated the influence of carbon black content on the dynamic crack growth behaviour of SBR and NR vulcanisates using pure shear-specimens. The comparison of the crack growth curves showed that, under the selected experimental conditions, the NR vulcanisates exhibited a significantly lower crack propagation speed at a comparable tear energy T than the SBR vulcanisates. The addition of the filler also resulted in a reduction in the crack propagation speed.

Carbon black-reinforced NR and HNBR vulcanisates were also investigated by Kim et al. [18]. They also used pure shear-specimens for the cyclic fracture mechanics tests on carbon black-reinforced NR and HNBR materials. The test specimens were loaded with different amplitudes between 25 and 200 % at a frequency of 1 Hz. The number of cycles was set at 10,000 and the crack size was determined after the test. The crack growth rate was determined from this data. Carbon blacks with different activities were used as fillers. The results of the fracture mechanics tests on the NR vulcanisates showed that the composition of the mixture, particularly with regard to the filler content, has a significant influence on the crack growth rate with a comparable energy release rate. The filler type did not have a very strong effect on the crack growth curves of the NR materials under the selected test conditions.

Yuanbo Liu et al. [19] also carried out cyclic fracture mechanics tests. The aim was to evaluate the influence of the filler or filler system based on carbon black and organically modified montmorillonite on the mechanical and fracture mechanics properties. Metal blade notched SENT-specimens were used for the cyclic fracture mechanics tests and maximum strains of 30 % were applied. The stress was sinusoidal and applied at a frequency of 3 Hz. The results of the tests showed that the smaller the increase m in the crack growth curve in area 2, the greater the resistance to fatigue crack propagation. With the investigations, the authors have shown, among other things, that a filler combination of carbon black and OMMT can have a positive effect on the rise m, i.e. the fatigue crack resistance becomes greater, although at the same time there is an increase in the crack growth rate with comparable crack energy. Additional energy-dissipating processes due to the presence of the OMMT layers are discussed as the cause.

See also

• Fatigue
• Pure shear-specimen
• Crack resistance curve – Experimental methods
• Ageing elastomers
• Rebound resilience elastomers

References

[1]	Reincke, K.: Elastomere Werkstoffe – Zusammenhang zwischen Mischungsrezeptur, Struktur und mechanischen Eigenschaften sowie dem Deformations- und Bruchverhalten, Habilitation, Martin-Luther-Universität Halle-Wittenberg, Shaker Verlag (2016) (ISBN 978-3-8440-4637-3; see AMK-Library under B 2-2)
[2]	Eisele, U., Kelbch, S., Engels, H.‐W.: The Tear Analyzer – A New Tool for Quantitative Measurements of the Dynamic Crack Growth of Elastomers. Kautsch. Gummi Kunstst. 45 (1992) 1064–1069
[3]	Krause, K.‐H., Mennig, G.: Ermüdungsprüfung an Gummi. Tagungsband TECHNOMER 99, Chemnitz (1999) (ISBN 3-00-004710-7)
[4]	Stoček, R., Heinrich, G., Gehde, M., Kipscholl, R.: (2013). Analysis of Dynamic Crack Propagation in Elastomers by Simultaneous Tensile- and Pure-Shear-Mode Testing. In: Grellmann, W., Heinrich, G., Kaliske, M., Klüppel, M., Schneider, K., Vilgis, T. (Eds): Fracture Mechanics and Statistical Mechanics of Reinforced Elastomeric Blends. Lecture Notes in Applied and Computational Mechanics, Vol. 70. Springer Berlin Heidelberg (2013) pp 269–301; https://doi.org/10.1007/978-3-642-37910-9_7
[5]	Stoček, R., Heinrich, G., Gehde, M.: The Influence of the Test Properties on Dynamic Crack Propagation in Filled Rubbers by Simultaneous Tensile‐ and Pure‐Shear‐Mode Testing. In: Heinrich, G., Kaliske, M., Lion, A., Reese, S., (Eds.): Constitutive Models for Rubber VI, CRC Press (2009) 345–352
[6]	Krause, K.‐H.: Gepulste Risswachstums‐Prüfungen an Gummiwerkstoffen. TECHNOMER 97, Chemnitz (1997) (ISBN 3-00-001942-1)
[7]	Ziegler, C., Baaser, H., Häusler, O.: Fatigue and Crack Growth Behavior of Rubber Products. In: Boukamel, A., Laiarinandrasana, L., Méo, S., Verron, E. (Eds.): Constitutive Models for Rubber V, Taylor & Francis Group London (2008) 197–202
[8]	Stoček, R.: Dynamische Rissausbreitung in Elastomerwerkstoffen. Dissertation, Technische Universität Chemnitz (2012)
[9]	Coesfeld: Materialprüfgeräte für Industrie und Forschung. (access: 22.01.2023)
[10]	Clamroth, R., Eisele, U.: Untersuchungen zur Weiterreißfestigkeit und Beständigkeit gegen Rissbildung. Kautsch. Gummi Kunstst. 28 (1975) 433–440
[11]	Blumenauer, H.: Werkstoffprüfung. 6th Edition, Deutscher Verlag für Grundstoffindustrie, Leipzig (1994) (ISBN 3-342-00547-5; see AMK-Library under M 3)
[12]	Eisele, U.: Introduction to Polymer Physics. Springer, Berlin Heidelberg (1990) (ISBN 978-3-642-74436-5)
[13]	Stevenson, A.: Fatigue and Fracture of Rubber in Engineering Applications. Paper for Educational Symposium. 145th Technical Meeting of the Rubber Division, ACS, Chicago April 19–22, 1994
[14]	Aglan, H., Moet, A.: The Resistance of Rubber Compounds to Brittle Crack Propagation. Rubber Chem. Technol. 62 (1989) 98–106 DOI: [1]
[15]	Young, D. G., Danik, J. A.: Effects of Temperature on Fatigue and Fracture. Rubber Chem. Technol. 67 (1994) 137–147 DOI: [2]
[16]	Reincke, K., Lach, R., Grellmann, W., Henrich, G.: Investigation of Crack Propagation Behaviour of Unfilled and Filled Vulcanizates. In: Grellmann, W., Seidler, S. (Eds.): Deformation and Fracture Behaviour of Polymers. Springer Berlin Heidelberg (2001) 493–504; (ISBN 3-540-41247-6; see AMK-Library under A 7)
[17]	Papadopoulos, I. C., Thomas, A. G., Busfield, J. J. C.: Rate Transitions in the Fatigue Crack Growth of Elastomers. J. Appl. Polym. Sci. 109 (2008) 1900–1910 DOI: [3]
[18]	Wonho Kim, Minyoung Kim, Young‐Wook Chang, Jung‐Eun Shin, Jong‐Woo Bae: Fatigue Crack Growth Behavior of NR and HNBR Based Vulcanizates with Potential Application to Track Pad for Heavy Weight Vehicles. Macromol. Res. 11 (2003) 73–79 DOI: [4]
[19]	Yuanbo Liu, Li Li, Qi Wang, Xin Zhang: Fracture Properties of Natural Rubber Filled with Hybrid Carbon Black/Nanoclay. J. Polym. Res. 18 (2011) 859–867 DOI: [5]