Strain Hardening Test (SHT)
| A service provided by |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Our further education offers: https://www.psm-merseburg.de/weiterbildung |
| PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Strain hardening test (SHT)
Methods for describing long-term behaviour as resistance to slow crack propagation
Conventional methods such as the Full Notch Creep Test (FNCT) or the Pennsylvania Edge Notch Tensile (PENT) Test for testing the long-term behaviour as resistance to slow crack growth (SCG) are becoming increasingly unsuitable for highly developed polymer pipe materials due to the extremely long test times of often more than one year. For this reason, there is an urgent need to develop new, time-saving test methods for estimating the service life of these polymer materials. One possible solution to this problem is the implementation of new test methods.
Experimental method and parameters
In 2008, SABIC presented an elegant method for predicting slow crack growth using simple tensile tests at higher temperatures, known as the Strain Hardening Test (SHT) (standardised according to ISO 18488 [1]). For a given material, the slope of the stress–strain diagram in the strain hardening range correlates very well with the results obtained from the FNCT [2].
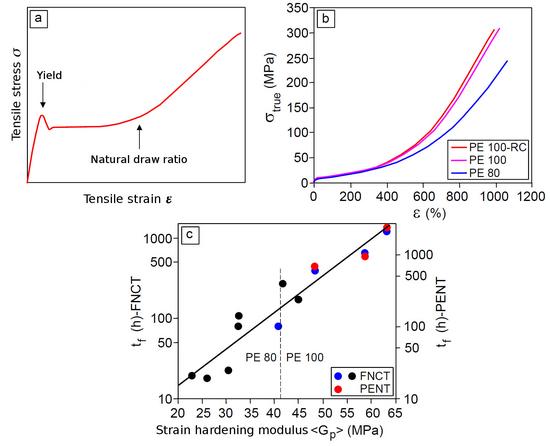
The SHT is based on the uniaxial tensile test at a deformation rate of 20 mm/min and a temperature of 80 °C. The stress–strain diagrams (Fig. 1a) are measured and further analysed (see also [3, 4]).
The strain ratio λ is calculated from the current length l and the initial specimen length l0 between the measuring marks to λ = 1 + Δl/l0, where Δl = l0 – l is the specimen elongation. The true stress σtrue is calculated according to σtrue = λ · F/A, where F is the measured force and A is the product of the initial width and thickness. The Neo-HOOKE material law is used to fit and extrapolate the data, from which the strain hardening (SH) modulus <Gp> for 8 < λ < 12 is calculated according to
| . | (1) |
Here, C is a mathematical parameter of the material law that describes the extrapolation of the tensile stress to λ = 0.
Application of SHT for PE pipe materials
The test method for estimating the SH modulus was applied to various generations of PE materials such as PE 80 (two types: PE-HD, PE-MD – medium-density polyethylene), PE 100 (three types from two manufacturers) and PE 100-RC (one type). For each material, five test specimens (modified type 3 according to ISO 37) were punched out of a 1 mm thick compression-moulded plate. The measurement was carried out using an Instron 6025R5800 universal testing machine with a temperature control chamber and video strain gauge in accordance with the test conditions specified in ISO 18488.
The true stress–strain diagrams shown in Fig. 1b for some PE-HD pipe types show no signs of a geometrically induced stress reduction after the yield point (as in Fig. 1a). The SH modulus is shown in Figure 1c in relation to the failure time from the FNCT and PENT. Both the increase in the true stress–strain diagrams and the SH modulus of PE-HD correlate with the resistance to SCG, which increases in the order PE 80 → PE 100 → PE 100-RC according to [2–4].
| Fig. 1: | Stress–strain diagram of PE-HD (a). True stress–strain diagram (b) for PE-HD pipe types [3, 4] and failure time tf as a function of SH modulus (c): black dots [2], blue and red dots [3, 4] |
Outlook
Due to the enormous amount of time required for FNCT and PENT as conventional methods for assessing long-term performance and service life, new test methods such as the strain hardening test must be implemented. Figure 1c shows the failure time plotted against the SH modulus. A highly non-linear relationship (R2 = 0.89) – by no means a linear one, as assumed in [2] (cf. however [5, 6]) – exists between <Gp> and tf, which can be empirically described for the FNCT by
| (2) |
(<Gp> in MPa, tf in h) for the FNCT. In accordance with [2], in which a boundary line for identifying PE 100 and PE 100-RC was found, a similar boundary line in Figure 1c at <Gp> = 41 – 42 MPa separates the SCG resistance data of PE 80 from that of PE 100 [3, 4].
See also
References
| [1] | ISO 18488 (2015-09): Polyethylene (PE) Materials for Piping Systems – Determination of Strain Hardening Modulus in Relation to Slow Crack Growth – Test Method |
| [2] | van der Stock, E., Scholte, F.: Strain Hardening Test on PE Pipe Materials. In: Proceedings of Plastic Pipes XVI, Barcelona (2012), pages 10 |
| [3] | Nezbedova, E., Hodan, J., Kotek, J., Krulis, Z., Hutar, P., Lach, R.: Lifetime of Polyethylene (PE) Pipe Materials – Prediction using Strain Hardening Test. In: Grellmann, W., Langer, B. (Eds.): Deformation and Fracture Behaviour of Polymer Materials. Springer, Berlin (2017) 203–210 (ISBN 978-3-319-41877-3, see AMK-Library under A 19) https://springer.com/book/10.1007/978-3-319-41879-7 |
| [4] | Lach, R., Nezbedova, E., Langer, B., Grellmann, W.: Schnelle Abschätzung des mechanischen Langzeitverhaltens moderner Werkstoffe für Kunststoffrohre mittels des einachsigen Zugversuchs. In: Frenz, H., Langer, J. B. (Eds.): Fortschritte in der Werkstoffprüfung für Forschung und Praxis. Prüftechnik – Kennwertermittlung – Schadensvermeidung. Proceedings „Werkstoffprüfung 2017“, 30.11./01.12.2017, Berlin, pp. 259–264 (ISBN 978-3-9814516-7-2; see AMK-Library under A 20) |
| [5] | Deblieck, R., van Beek, D. J. M., Remerie, K., Ward, I. M.: Failure Mechanism in Polyolefines. The Role of Crazing, Shear Yielding and the Entanglement Network. Polymer 52 (2011) 2979–2990 |
| [6] | Kurelec, L., Teeuwen, M., Schoffeleers, H., Deblieck, R.: Strain Hardening Modulus as a Measure of Environmental Stress Crack Resistance of High Density Polyethylene. Polymer 46 (2005) 6369–6379 |