BOLTZMANN's Superposition Principle
BOLTZMANN'sches Superpositionsprinzip | A service provided by |
|---|
|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Our further education offers: https://www.psm-merseburg.de/weiterbildung |
| PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
A-Bild-Technik
Laws of viscoelasticity
BOLTZMANN's superposition principle, named after the Austrian physicist Ludwig Boltzmann (1844–1906), together with the correspondence principle and the time–temperature shift law, is used to describe the linear-viscoelastic behaviour of plastics [1].
Principle of superposition for relaxation and retardation
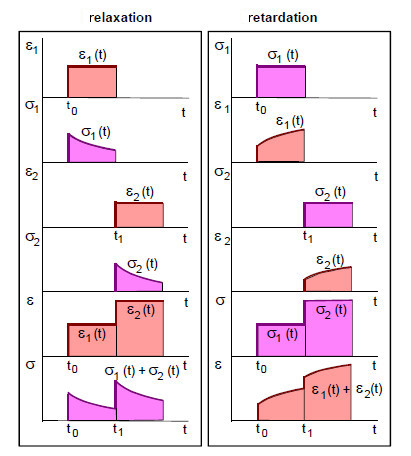
Figure 1 illustrates these relationships using diagrams of relaxation and retardation experiments.
| Fig. 1: | BOLTZMANN's superposition principle for relaxation and retardation cases |
BOLTZMANN's superposition principle describes the influence of mechanical history on the material behaviour of plastics. It states that the time-dependent effects of successive changes in the stress state add up linearly and summarily to the overall effect.
Basic assumptions
If the strain ε1(t) generates a stress σ1(t) and ε2(t) generates the stress σ2(t), then the sum ε1(t) + ε2(t) causes the total stress σ1(t) + σ2(t).
Conversely,
if the stress σ1(t) produces the strain ε1(t) and σ2(t) produces the strain ε2(t), then the sum σ1(t) + σ2(t) corresponds to the total strain ε1(t) + ε2(t).
The principle therefore takes into account relaxation and retardation, or the creep of plastics. The BOLTZMANN superposition principle is illustrated graphically in the schematic diagram in Fig. 1.
Based on this principle, the time-dependent deformation caused by applied loads (and vice versa) can be determined at different times with a reasonable amount of computational effort in the area of linear-viscoelastic material behaviour.
See also
References
| [1] | Lüpke, T.: Fundamental Principles of Mechanical Behavior. In: Grellmann, W., Seidler, S. (Eds.): Polymer Testing. Carl Hanser, Munich (2022) 3rd Edition, pp. 82/83 (ISBN 978-1-56990-806-8; E-Book: ISBN 978-1-56990-807-5; see AMK-Library under A 22) |