ICIT – Experimental Conditions

Sprachauswahl/Language selection

Dieser Artikel ist auch auf Deutsch verfügbar IKBV Experimentelle Bedingungen

A service provided by
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Our further education offers: https://www.psm-merseburg.de/weiterbildung
PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

ICIT – Experimental conditions

General

For the fracture mechanics evaluation of impact load (F)–deflection (f) diagrams from the instrumented Charpy impact test, compliance with experimental conditions is a necessary prerequisite. Of decisive importance here is the determination of the beginning of unstable crack propagation and the transition from elastic to elastic‒plastic material behaviour [1].

Control of maximum load, fracture time and impact energy

A fracture mechanics evaluation according to the criteria of linear-elastic fracture mechanics (LEFM) requires that the maximum load F_max according to Eq. (1) must always be greater than the amplitude of the inertial acceleration or impact pulse,

$F_{max}>F_{1}$

(1)

which is also referred to as the inertial load F₁. A proven technique for fulfilling this condition is to reduce the pendulum hammer velocity v_H (see: ICIT – Energy method) [2‒4]. To do this, it is only necessary to reduce the drop height of the pendulum hammer, which simultaneously reduces the energy of the pendulum and decreases the pendulum hammer velocity. The fracture mechanics parameters are determined from the maximum impact load using static evaluation formulas. To ensure a quasi-static stress state in the specimen, the fracture time t_B must be greater than 2.3 [4] to 3 times [5] the period of the characteristic inertial oscillation τ, i.e.

$t_{B}\geq 2,3\;...\;3\tau$

(2)

where [6, 7] suggest a further reduction to 2τ or 1.5τ. This assumption is particularly important for fracture mechanics investigations, depending on the test velocity and test temperature.

In addition to the relationship between impact load and inertial load as well as the fracture time and the period of the inertial oscillation, the energy absorption during the impact process must also be controlled.

The impact energy A_H introduced by the pendulum hammer for the fracture process must be greater than three times the total deformation energy A_G consumed by the test specimen.

$A_{H}>3A_{G}$

(3)

Control of the electronic measuring chain of the ICIT device system

To avoid misinterpretation of the material behaviour, it is necessary to check the electronic measuring chain of the device system used for the instrumented Charpy impact test to ensure that no additional oscillations (disturbance oscillations) that are not caused by the material behaviour are superimposed on the experimentally determined relationship between impact load and deflection. These are natural oscillations of the coupled mechanical system consisting of the specimen, pendulum hammer and support, and high-frequency signal oscillations caused by reflected sound waves or by the measuring setup of the device system [1] (see also: impact loading pendulum impact tester).

To check the frequency response of the electronic measuring chain, the condition according to Eq. (4) applies to the rise time t_R

$t_{B}>1,1\,t_{R}$

(4)

with t_R ‒ rise time of the electronic measuring chain (amplifier and frequency filter).

$t_{R}={\frac {0,35}{f_{0,915}}}\;\;\;\;\;\;;\;\;\;\;\;\;t_{R}={\frac {0,27}{f_{0,707}}}$

f_0,915dB ‒ frequency at which amplitude is 90 %

f_0,707dB ‒ frequency at which amplitude is 70 %

When using electronic frequency filtering, equation (5) must be observed as a condition for frequency filtering to occur [8].

$t_{R}\geq 1,4\,\tau$

(5)

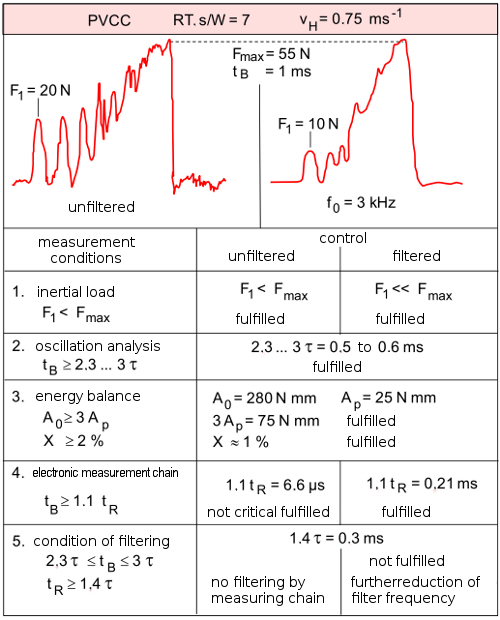
Example of compliance with the experimental conditions

Using the example of a chlorinated PVC material (abbreviation: PVC-C), compliance with all experimental conditions was verified in [1], whereby the unfiltered and filtered impact load‒deflection signal was recorded in parallel on a test specimen using a special measuring setup [9].

Taking into account the filter conditions according to Eq. (5) [8], the filter frequencies of 3 and 4 kHz specified in [1] have proven to be suitable for practical applications with plastics, whereby rise times of t_R = 0.2 ms even allow a further reduction of the filter frequency. For the unfiltered signal, the experimental conditions can be easily met with rise times t_B ~ 6 µs, which are very small compared to the fracture times of plastics (t_B ~ 1 ms). For filled polymer materials, filtering is unsuitable in cases where the change in crack propagation energy is to be considered, as this results in a significant distortion of this energy value.

To improve the evaluability of the impact load‒deflection signals, mechanical damping elements are used in addition to electronic filtering, some of which are also recommended in standards. Here, sufficient control of the F‒f signals is necessary to avoid incorrect assessments of the material behaviour.

Fig. 1:

Control of experimental measurement conditions in instrumented notch impact tests using the example of a chlorinated PVC material (abbreviation: PVC-C)

See also

• Inertial load
• Frequency response control
• Instrumented Charpy impact test
• MPK-Procedure MPK-ICIT
• Impact loading pendulum impact tester

References

[1]	Grellmann, W.: Beurteilung der Zähigkeitseigenschaften von Polymerwerkstoffen durch bruchmechanische Kennwerte. Habilitation (1986), Technischen Hochschule Merseburg, Wiss. Zeitschrift TH Merseburg 28 (1986), No. 6, pp. 787‒788 (content, summary)
[2]	Retting, W.: Behaviour of plastic films under biaxial impact stressing, Materialprüfung 8 (1966) 2, S. 55‒60
[3]	Ortmann, R., Man, J.: Zur Bestimmung der dynamischen Bruchzähigkeit im registrierenden Kerbschlagbiegeversuch. Wiss. Zeitschrift TH Magdeburg 24 (1980) 1, p. 101
[4]	Holzmann, M., Man, J.: Dynamiká Lomová Houževnatost (Dynamische Bruchzähigkeit), Zvaranie (1977) 5–9, pp. 1‒43
[5]	Ireland, D. R.: Critical Review of Instrumented Impact Testing. Int. Conference on Dynamic Fracture Toughness, London (1976) Paper 5, 47–62
[6]	Ortmann, R.: TU Dresden, Weiterbildungszentrun Festkörpermechanik, Konstruktion und rationeller Werkstoffeinsatz, Studientexte Bruchmechanik II, No.3 (1983) p. 38
[7]	Rittinger, J.: Die Zuverlässigkeit der mit Instrumentenschlagversuch bestimmten dynamischen bruchmechanischen Kenngrößen. 8. Kongress Materialprüfung, 28.9.–1.10.1982, Budapest (1982) pp. 521–525
[8]	Server, W. L.: Impact Three-point Bend Testing for Notched and Precracked Specimens. Journal of Testing and Evaluation. JTEVA 6 (1978) 1, pp. 29–34 DOI: https://doi.org/10.1520/JTE10915J
[9]	Jungbluth, M.: Untersuchungen zum Einfluss der Prüfkörperdicke und der Temperatur auf die Zähigkeitseigenschaften von PVCC und PVC bei stoßartiger Beanspruchung. Diplomarbeit, Technische Hochschule Merseburg (1982) (see AMK-Library under B 3-11)