Correspondence Principle

Sprachauswahl/Language selection

Dieser Artikel ist auch auf Deutsch verfügbar Korrespondenzprinzip

A service provided by
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Our further education offers: https://www.psm-merseburg.de/weiterbildung
PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Correspondence principle

Classification

The correspondence principle is derived from BOLTZMANN's superposition principle. It provides the important practical statement that the solutions available from elasticity theory may be used in the linear-viscoelastic range. The prerequisite for this is that the viscoelastic deformations in plastics used in construction are very small. Since these solutions form the basis of all strength calculations, this greatly facilitates the use of plastics.

Fundamentals Correspondence principle

Instead of the stresses σ, the time-dependent stress function σ(t) is used; instead of the deformation ε, the time-dependent deformation ε(t) is used; and instead of the modulus of elasticity, the relaxation modulus E_r(t) or the creep modulus (see: creep behaviour determination) is used. However, instead of the relaxation or creep modulus, the reciprocal value, the compliance C(t) = 1/E_r(t) (C...compliance), is usually used.

This also applies, of course, to every other modulus (shear modulus and modulus of compressibility), every other stress and every other deformation. The time-dependent variables are interrelated by the relationships known from elasticity theory, whereby the time dependence of transverse contraction must also be taken into account.

Time and temperature dependence of modulus and Poisson's ratio

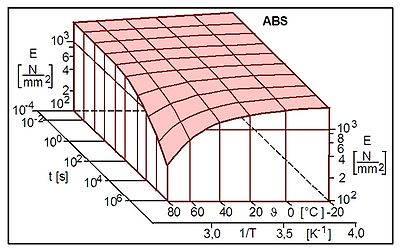
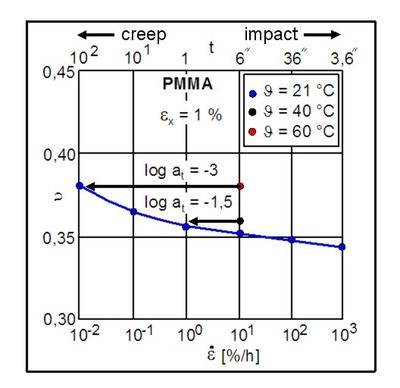
The following examples show the time and temperature dependence of the elastic modulus of acrylonitrile butadiene styrene (abbreviation: ABS) and the time dependence of the Poisson's ratio using poly(methyl methacrylate) (abbreviation: PMMA) as an example.

Fig. 1:

Time and temperature dependence of the modulus of elasticity for ABS according to Menges

Fig. 2:

Poisson's ratio as a function of strain rate ε˙ of PMMA under uniaxial deformation according to Menges

See also

• Elasticity
• Linear-viscoelastic behaviour
• BOLTZMANN's superposition principle
• Time–temperature shift law

References

• Menges, G.: Werkstoffkunde Kunststoffe. 3rd, completely revised and expanded edition, Carl Hanser, Munich Vienna (1990) p. 121, (ISBN 978-3-446-15612-8; see AMK-Library under G 11)
• Lüpke, T.: Fundamental Principles of Mechanical Behavior. In: Grellmann, W., Seidler, S. (Eds.): Polymer Testing. Carl Hanser, Munich (2022) 3rd Edition, pp. 84 (ISBN 978-1-56990-806-8; E-Book: ISBN 978-1-56990-806-5; see AMK-Library under A 22)