Bend Test – Influences

Sprachauswahl/Language selection

Dieser Artikel ist auch auf Deutsch verfügbar

A service provided by

Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Our further education offers: https://www.psm-merseburg.de/weiterbildung
PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Bend test – Influences

Elastic bending theory

The elastic line for large deflections w is described with the general differential equation of the elastic bending line of the deformed bending test specimen (2nd order theory), which is complicated to handle from an engineering point of view and can only be solved numerically (Eq. 1), since the

{\frac {w^{\prime \prime }(x)}{\left[1+w^{\prime 2}(x)\right]^{\frac {3}{2}}}}=-{\frac {M(x)}{EI}}

(1)

boundary conditions as well as the equation itself depend on the inclination of the bending line w'. For this reason, the relevant standards [2, 3] for bending tests on plastics dispense with the influence of the test specimen inclination and use the simplified first-order theory for the bending differential equation (Eq. 2).

w^{\prime \prime }(x)=-{\frac {M(x)}{EI}}

(2)

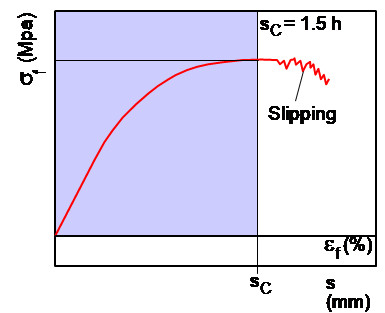
However, this simplified form of the differential equation of the bending is actually only for small deformations, i.e. the deflection is much smaller than the geometric dimensions (thickness). Due to the then only slight inclinations to the supports of the test specimen, the corresponding solutions can be used to calculate the characteristic values of the bending test. As the stress-strain curve is influenced by unavoidable slip effects at large deflections (Fig. 1), a limit value of 3.5 % peripheral fibre strain was specified in the original version of ISO 178, up to which bending tests can be carried out in accordance with the standard. Today, this value is referred to as conventional deflection s_C and is then 6 mm for a 4 mm thick test specimen [1]. In the current version of the standard for three-point bending tests on plastics [2], even values > 9 mm are permitted for the deflection, for which the first-order bending theory cannot actually provide valid results.

Fig. 1:

Slipping of specimen on the supports at greater deflection

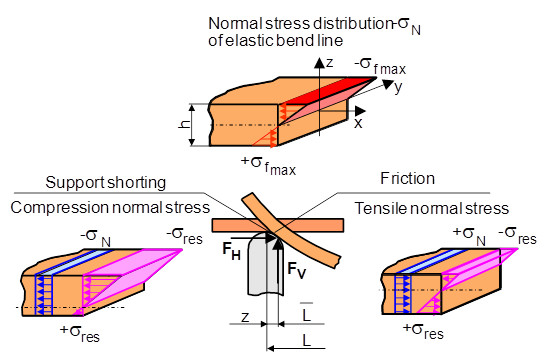
With the familiar equations of elastic bending theory, the errors resulting from the HERTZIAN pressure at the supports, the rolling of the test specimen on the support radius or the associated shortening of the support distance are of course neglected. A distinction can be made here between influencing factors that should actually be taken into account in the force signal and that are reflected in the calculated bend-ing stress, and measurement errors that are included in the deflection and conse-quently also in the edge fibre elongation. These influencing variables are illustrated in Figure 2.

Influences on the calculation of the bending stress

Fig. 2:

Influence of friction and shortening of support distance on the bend stress

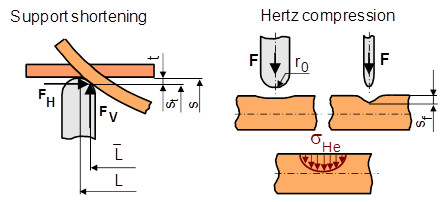
Figure 2 shows that the theoretically symmetrical stress distribution with respect to the test specimen cross-section is more strongly influenced by the normal stresses (tension and compression) with increasing radius of the support and larger deflections. Geometrically, this influencing variable can be expressed by the value z. The resulting stress σ_res can arise from the friction at the abutments or be caused by the shortening of the distance with the horizontal force F_H. The frictional force naturally depends on the pairing of the materials of the support and the analysed material, and must be determined experimentally. In both cases, an asymmetrical stress pro-file is created, whereby these effects overlap and cause a displacement of the neutral fibre that cannot be precisely predicted. In addition to these influencing factors, the HERTZIAN pressure under the support and the loading die can cause a compressive stress which, however, drops very quickly towards the centre of the test specimen and is therefore not considered further (Fig. 3).

Influences on the calculation of the periphal fibre strain

By using round supports, the impeded rolling of the test specimen on the bearing will also result in a differential displacement t, which depends on the deflection s or w (Fig. 3).

Fig. 3:

Influence of local compression and shorting of the support distance on strain

Assuming a crosshead travel measurement, the determined deflection and the resulting peripheral fibre strain are lower, which means that greater forces are required. As a result of the radius design, the measured signal may also include deflections w_f, which are indirectly dependent on the Hertzian pressure and also cause a smaller deflection. An approximate consideration of the listed influencing factors on the calculated bending stress is shown below using the example of three-point bending.

Calculation of bending stress in the three-point bending test

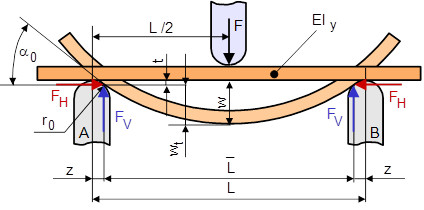
As can be seen in Figure 4, the resulting horizontal force F_H depends on the inclination of the support and leads to a normal compressive stress with respect to the cross-section and a corrected bending stress (Eq. 3), where W_b is the section modulus. In addition to the pure normal stress, F_H also causes an additional bending moment which is dependent on the resulting deflection. This corrects the resulting bending stress to Equation (3).

Fig. 4:

Consideration of influence of support shortening

The reduction in the support spacing is recorded in the bending moment via the correction factor z. The bending stress corrected in this respect depends, as expected, on the resulting deflection w and the abutment radius r₀. The consideration of all these different influencing factors leads to Equation (3):

\sigma _{f}={\frac {3FL}{2bh^{2}}}\left[1+{\frac {6w^{2}}{L^{2}}}-{\frac {hw}{L^{2}}}-{\frac {2r_{0}}{L}}sin\ arctan\left({\frac {3w}{L}}\right)\right]

(3)

In the case of deflection, the resulting error can be corrected relatively easily using the known value of z and the support geometry, resulting in the following correction equation. An analogue procedure is possible for four-point bending, although this results in more complicated correction equations.

\epsilon _{f}={\frac {{\frac {6hw}{L^{3}}}\left[L-2r_{0}sin\ arctan{\frac {3w}{L}}\right]^{3}-6hr_{0}\left[1-cos\ arctan{\frac {3w}{L}}\right]}{\left[L-2r_{0}sin\ arctan{\frac {3w}{L}}\right]^{2}}}\ 100\ \%

(4)

The correction equations given in the standard ISO 14125 [3] differ slightly from the solutions given above, but give almost identical results, whereby s is used here instead of w for the deflection. To take friction into account, the coefficient of friction µ must be determined experimentally (Eq. 6). The corrected bending stress in the three-point bending test is calculated according to Eq. (5).