Temperature Conductivity

Sprachauswahl/Language selection

Dieser Artikel ist auch auf Deutsch verfügbar Thermische Leitfähigkeit

A service provided by
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Our further education offers: https://www.psm-merseburg.de/weiterbildung
PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Thermal conductivity; Thermal diffusivity

Definition

From the physical point of view, a fundamental differentiation must be made between heat conductivity, which describes the transport of energy in a material, and temperature conductivity or thermal diffusivity.

The temperature conductivity a is that velocity at which temperature fields change in a material, and so describes the non-stationary thermal conduction. It is determined by the thermal conductivity λ, the specific thermal capacity c_p and by the mass density ϱ. The temperature conductivity is defined by

$a={\frac {\lambda }{\varrho ~c_{p}}}$

(1)

Derivation

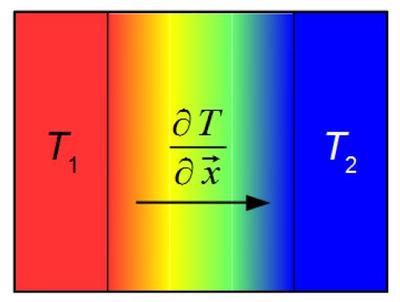
Given are two containers with the temperatures T₁ and T₂ and between them a transition medium in which the temperature gradient is present (Fig. 1). The heat flow thereby goes in the direction indicated by the arrow in the picture. The heat quantity Q₁ with the temperature T₁ flows in the transition medium to the container with the heat quantity Q₂ of the lower temperature T₂. This means that heat is transported through the transition medium. The heat flow has the form

${\dot {Q}}=m\cdot c_{p}\cdot {\frac {\partial T}{\partial t}}$

(2)

Considering now the property of the thermal conductivity of the transition medium, then (A is the heat transfer area) also applies:

${\dot {Q}}=-\lambda \cdot A~{\frac {\partial T}{\partial x}}$

(3)

Figure 1:

Schematic illustration of the temperature gradient between the containers with temperatures T1 and T2 with the transition medium

The equation of Eq. (2) and Eq. (3) does not yet yield the temperature conductivity. For this, the general form of these equations must be used:

Instead of the heat flow, the heat flow density vector j is considered, which is the heat flow through a cross-sectional area that can be calculated with the 1st Fourier's law according to Eq. (4).

${{\boldsymbol {j}}=-\lambda \cdot \mathrm {grad} ~T}$.

(4)

The heat flow per volume which the container loses with T₁ is according to Eq. (2)

${{\dot {q}}=\varrho \cdot c_{p}\cdot {\frac {\partial T}{\partial t}}}$.

(5)

According to the continuity equation, the following applies to heat transport

${{\frac {\partial q}{\partial t}}=-\mathrm {div} \ {\boldsymbol {j}}}$.

(6)

After entering Eq. (4) and Eq. (5) into Eq. (6), the continuity equation obtains the form

${{\frac {\partial T}{\partial t}}={\frac {\lambda }{\rho \cdot c_{p}}}\cdot {\frac {\partial ^{2}T}{\partial x^{2}}}}$.

(7)

with which again Eq. (1) is obtained (2nd Fourier's law).

Practical Aspects

The temperature conductivity is a property of the respective material and is listed here in Table 1 for a selection of thermoplastics. This characteristic value describes the non-stationary heat transport. For example, it is important that the handles of the vessels containing the hot liquid have a lower thermal conductivity in order to reduce the risk of injury when handling them. Furthermore, this parameter is used for the fire safety of materials and the assessment of heat storage.

Table 1: Temperature conductivity of some selected thermoplastics

Material	Temperature conductivity α (mm2/s)
PVC-U	0.122
PVC-P	0.145
PE-HD	0.227
PP	0.145
PS	0.115
POM	0.161

Importance

Since the temperature conductivity indicates the velocity at which a temperature spreads through a medium, it is fundamental for studies on heat transport in media. This characteristic value is used in the building's industry, e.g. for the thermal insulation of buildings. Moreover, temperature conductivity is easier and more accurate to measure than thermal conductivity, therefore thermal conductivity is often determined indirectly via temperature conductivity.

References

[1]	Landau, L. D., Lifschitz, E. M.: Hydrodynamik – Lehrbuch der theoretischen Physik. Akademie-Verlag, Berlin (1991)
[2]	https://www.linseis.com: Wärmeleitfähigkeit/Temperaturleitfähigkeit (access: 01.04.2025)
[3]	Marek, R., Nitsche, K.: Praxis der Wärmeübertragung. Grundlagen – Anwendungen – Übungsaufgaben. 2., aktualisierte und erweiterte Auflage, Fachbuchverlag Leipzig im Carl Hanser Verlag, München (2010) (ISBN 978-3-446-42510-1; see AMK-Library under I 43)
[4]	Paus, H.: Physik in Experimenten und Beispielen. Carl Hanser Munich Vienna (1995), p. 580 f. (ISBN 3-446-17371-4; see AMK-Library under I 4)
[5]	Domininghaus, H., Elsner, P., Eyerer, P., Hirth, T.: Kunststoffe. Eigenschaften und Anwendungen. 8. Auflage, Springer, Heidelberg (2012), p. 304 (ISBN 978-3-642-16172-8 ; see AMK-Library under G 41)

Standards Reference

• ISO 22007-2 (2022-06): Plastics — Determination of Thermal Conductivity and Thermal Diffusivity — Part 2: Transient Plane Heat Source (Hot Disc) Method