ICIT – Limits of Fracture Mechanics Evaluation

Sprachauswahl/Language selection

Dieser Artikel ist auch auf Deutsch verfügbar IKBV Grenzen bruchmechanischer Bewertung

A service provided by
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Our further education offers: https://www.psm-merseburg.de/weiterbildung
PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

ICIT Limits of fracture mechanics evaluation

Requirements for the loading conditions

In order to use the instrumented Charpy impact test to solve problems in materials development and optimisation, the loading conditions (see also stress) must be adapted so that as many plastics and composite materials as possible are assessed under exactly the same loading conditions [1].

Of particular importance is the knowledge of the relationships between individual stress conditions with regard to a standardisation of the method with the aim of a fracture mechanical characterisation of the toughness [2, 3].

Influence of the notch depth, the pendulum hammer speed and the support distance

In addition to the influence of the notch depth (see also: J-integral evaluation methods (overview)) and the pendulum hammer velocity v_H (see: ICIT ‒ Influence of pendulum hammer velocity) on the shape of the impact loads (F)‒deflection (f)-diagrams and the material behaviour, the influence of the support span of the test specimen bearings on the measured variables must also be taken into account.

While fracture mechanically evaluable F‒f diagrams were obtained for polypropylene in the entire a/W and s/W range for v_H = 1 ms^-1 in [1], for a large number of materials, in particular high-impact polymer materials and modified, i.e. filled and reinforced polymer materials, depending on the material structure, a limit of the fracture mechanical evaluation possibility is already reached at room temperature. Even a higher electronic reinforcement cannot provide any material information, as the maximum impact load is too small in comparison with the superimposed vibration (see: ICIT ‒ experimental conditions). A further problem for filled and reinforced plastics is that often no unstable crack propagation occurs.

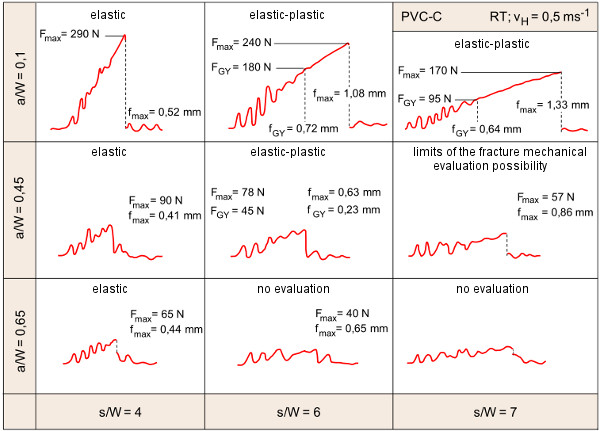
To derive the general relationships, two material examples for chlorinated PVC (abbreviation: PVC-C) and polyamide 6 (abbreviation: PA 6) were explained in [1]. Figure 1 shows the F–f diagrams for selected a/W and s/W ratios at the lowest possible pendulum hammer velocity (v_H = 0.5 ms^-1) at room temperature.

Fig. 1:

Limit of the fracture mechanics evaluation possibility for chlorinated PVC (abbreviation: PVC-C) (RT; vH = 0.5 ms-1)

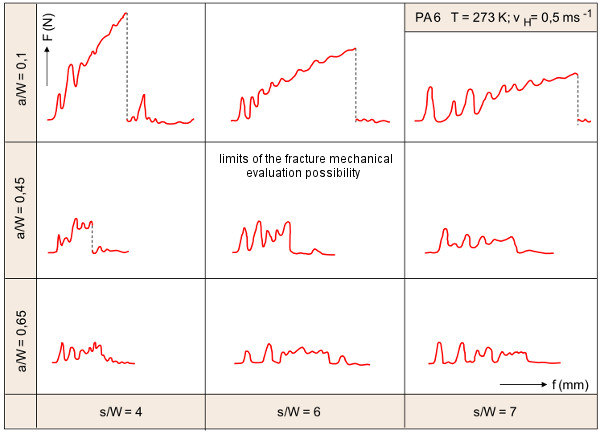
Figure 2 shows the F-f diagrams recorded in instrumented Charpy impact test for polyamide 6 (abbreviation: PA 6) for different a/W and s/W ratios at a pendulum hammer speed of v_H = 0.5 ms^-1 at T = 273 K.

Fig. 2:

Limit of the fracture mechanics evaluation possibility of the impact load‒deflection diagrams of polyamide 6 abbreviation: PA 6 with variation of the a/W and s/W ratio

Limits of the fracture mechanics evaluation possibility

It is clear from the examples shown:

1. the maximum impact load F_max decreases with increasing a/W and s/W
2. the inertial load F₁ is independent of a/W and s/W
3. the period of the inertial oscillation period τ increases with increasing s/W
4. with increasing a/W and s/W, the relationship F_max > F₁ becomes increasingly difficult to fulfil and at the same time the better fulfilment of the relationship t_B > 2.3…3 τ becomes meaningless.

While for PVC-C the limit of the fracture mechanical analysability of the diagrams is reached for a/W = 0.45 and s/W = 7, for example, for the PA 6 material this is already at lower stress conditions (T = 273 K; v_H = 0.5 ms-1; a/W = 0.45; s/W = 6).

Optimisation of the signal shape for fracture mechanics evaluation

With regard to obtaining optimum signal shapes for a fracture mechanics evaluation in compliance with the control conditions formulated for ICIT – Experimental conditions according to Eq. (1) to Eq. (3) for the instrumented Charpy impact test, the demand for s/W = 4, a low a/W ratio and a low pendulum hammer velocity is derived from the results presented. This provides generally applicable loading conditions for a large number of applications, if the applicability of the fracture mechanics concepts for describing toughness is also proven for low a/W ratios. A further advantage of using low support distances of the abutments lies in the restriction of the possibilities of pull-through. This is particularly important for plastics with high impact strength, which naturally exhibit high deflections.

See also

• Instrumented Charpy impact test (ICIT)
• MPK-Procedure MPK-ICIT
• Impact test
• ICIT – Extended stop-block method
• Impact loading plastics

References

[1]	Grellmann, W.: Beurteilung der Zähigkeitseigenschaften von Polymerwerkstoffen durch bruchmechanische Kennwerte. Habilitation (1986), Technischen Hochschule Merseburg, Wiss. Zeitschrift TH Merseburg 28 (1986), H. 6, S. 787–788 (Inhaltsverzeichnis, Kurzfassung)
[2]	ISO 179-2 (2020-05): Plastics ‒ Determination of Charpy Impact Properties ‒ Part 2: Instrumented Impact Test
[3]	MPK-Procedure MPK-ICIT (2016-10): Testing of Plastics – Instrumented Charpy Impact Test: Procedure for Determining the Crack Resistance Behaviour Using the Instrumented Impact Test