Dielectric Loss Factor

Sprachauswahl/Language selection

Dieser Artikel ist auch auf Deutsch verfügbar Dielektrischer Verlustfaktor

A service provided by
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Our further education offers: https://www.psm-merseburg.de/weiterbildung
PSM on Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Dielectiric loss factor

Fundamentals

An electric field exerts forces on a plastic (dielectric) that influence the molecular electrostatics and lead to a charge shift between adjacent potential surfaces. This is associated with a polarisation of the dielectric, which is an essential property of the plastic material. The following section discusses the basic measurement setup for dielectric spectroscopy [1, 2] and the determination of the dielectric loss factor.

Measurement setup

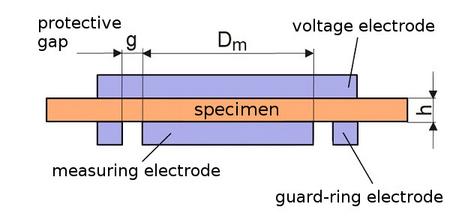
A plate capacitor with a concentric electrode arrangement and variable gap thickness is used as the measuring device. Its basic design is shown in DIN 62631 [3] (Fig. 1). The ring-shaped guard electrode ensures a homogeneous electric field in the area of the measuring electrode [3–6].

Fig. 1:

Schematic diagram of the measuring capacitor according to [3]

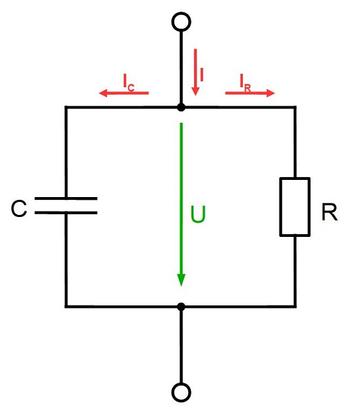
When an alternating field is applied, the phase shift between the ohmic resistance and the capacitive resistance causes a loss of electrical energy, which is converted into heat. In an ideal capacitor, only reactive energy is converted. This is the energy that does not appear externally, meaning that no energy is drawn from the circuit. Real capacitors also have active power due to the presence of the dielectric. Therefore, ohmic resistance must be taken into account when calculating the loss factor.

Fig. 2:

Equivalent circuit diagram of a real capacitor

Figure 2 shows the equivalent circuit diagram as a parallel connection of a capacitor and an ohmic resistor. Using KIRCHHOFF's node theorem and the current-voltage relationship, the complex impedance of this circuit is determined according to Eq. (1).

${\frac {1}{Z}}={\sqrt {{\frac {1}{R^{2}}}+(\omega \cdot C)^{2}}}$

(1)

Determination of the characteristic value for dielectric loss

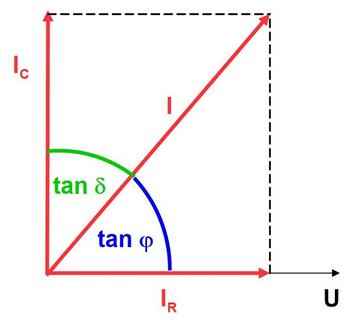
The equivalent circuit diagram in Fig. 2 yields the current–vector diagram shown in Fig. 3. The phase angle φ can then be specified in accordance with Eq. (2).

$\tan \varphi ={\frac {Im(I)}{Re(I)}}=\omega \cdot R\cdot C$

(2)

Due to the small deviation of the current vector I from the imaginary axis (I_C) in practice, the angle δ between this axis and the resulting axis is used as the loss factor or angle according to Eq. (3) [5].

$\tan \delta ={\frac {1}{\omega \cdot R\cdot C}}$

(3)

Fig. 3:

Current–vector diagram for the equivalent circuit diagram of the real capacitor

With the help of Eq. (3), the loss factor tan δ can be easily determined if the ohmic resistance can be measured. This describes the energy loss of the dielectric that occurs when an alternating voltage is applied during the reversal of polarisation. The dielectric loss in the form of the loss factor is therefore a measured variable that can represent changes in properties with a high degree of sensitivity.

See also

• Dielectric properties
• Volume resistance

References

[1]	Busse, G.: Dielectric Spectroskopy. In: Grellmann, W., Seidler, S. (Eds.): Polymer Testing. Carl Hanser, Munich (2022) 3rd Edition, pp. 453–454 (ISBN 978-1-56990-806-8; E-Book: ISBN 978-1-56990-807-5; see AMK-Library under A 22)
[2]	Schönhals, A.: Electrical and Dielectrical Properties. In: Grellmann, W., Seidler, S. (Eds.): Polymer Testing. Carl Hanser, Munich (2022) 3rd Edition, pp. 330–368 (ISBN 978-1-56990-806-8; E-Book: ISBN 978-1-56990-807-5; see AMK-Library under A 22)
[3]	DIN EN IEC 62631-2-1 (2018-12): Dielectric and Resistive Properties of Solid Insulating Materials – Part 2-1: Relative Permittivity and Dissipation Factor – Technical Frequencies (0.1 Hz to 10 MHz) – AC Methods. (IEC 62631-2-1:2028)
[4]	DIN IEC 60093 (1993-12): Methods of Test for Insulating Materials for Electrical Purposes – Volume Resistivity of Solid Electrical Insulating Materials. VDE 0303-30:1993-12 (withdrawn; replaced by DIN EN 62631-3-1 (2023-10); DIN EN 62631-3-2 (2023-01))
[5]	DIN EN IEC 62631-3-1 (2023-10): Dielectric and Resistive Properties of Solid Insulating Materials – Part 3-1: Determination of Resistive Properties (DC Method) – Volume Resistance and Volume Resistivity – General Method.VDE 0307-3-1:2023-10 (IEC 62631-3-1:2023)
[6]	DIN EN IEC 62631-3-2 (2023-01): Dielectric and Resistive Properties of Solid Insulating Materials – Part 3-2: Determination of Resistive Properties (DC Method) – Surface Resistance and Surface Resistivity. VDE 0307-3-2:2024-10 (IEC 62631-3-2:2023)
[7]	Lindner, H., Siebke, W., Simon, G., Wuttke, W.: Physik für Ingenieure. Fachbuchverlag Leipzig im Carl Hanser Verlag (2006), 17th Edition, (ISBN 978-3-446-40609-4) (see AMK-Library under I 56)